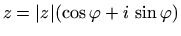Teil 6: Vom Komplexen ins Chaos, Abschnitt 5: Das Chaos im Feigenbaumdiagramm

In den letzten Posts ist deutlich geworden, dass die Entwicklung einer Zahlenreihe (bisher war es der prozentuale Anteil der Kaninchenpaare an der maximal möglichen Zahl, aber eigentlich haben wir nur Zahlenfolgen zwischen 0 und 1 generiert...) sich komplett anders gestaltet, wenn man einen quadratischen Term hinzufügt:

Je nach a strebt die Folge der Zahlen x gegen eine feste Zahl (nennt man das auch einen stabilen Punkt oder Attraktor), gegen abwechselnd 2 oder 4 oder 8...Zahlen oder es lässt sich überhaupt kein Endwert ausmachen.
Im letzten Fall hängt die Entwicklung extrem vom Startwert ab.

Solche nichtlinearen Terme erzeugen immer unter bestimmten Umständen chaotisches Verhalten.
Im nächsten Post sage ich dazu noch etwas mehr.

Die Physik, die man in der Schule und größtenteils auch im Studium lernt, ist alles lineare Physik.

Die Welt aber ist nichtlinear, chaotisch! Lineares Beschreiben kann immer nur eine Annäherung an das echte Verhalten der Welt sein.

Das ist einigen Pionieren wie Feigenbaum und Mandelbrot schon vor Jahrzehnten klar gewesen. Aber erst in diesem Jahrtausend hat es sich langsam durchgesetzt.
Als ich erstmalig mich um die Jahrhundertwende mit chaotischen Systemen beschäftigt habe, gab es noch viele Veröffentlichungen und Bücher, die zeigten, dass das seltsame Verhalten chaotischer Systeme dadurch entsteht, dass die Computer nicht genau genug rechnen könnten.

Wir wissen heute, dass das nicht der Fall ist. Die Welt als solches ist ein chaotisches Ssystem

Warum kommt sie uns so geordnet vor?

Weil Chaos und Ordnung keine Gegensätze sind, sondern innerhalb chaotischen Verhaltens auch immer Ordnungssturkturen entstehen..
Das sieht man wunderbar am Feigenbaumdiagramm: Ganz plötzlich endet das wirre Verhalten der Endpunkt und es gibt Bereiche, in denen nur ein oder zwei Endzustände entstehen. Ordung herrscht vor. Ändert man die Zahl a weiter, stellt sich sofort wieder Chaos ein.

So ist die Welt: Aus Chaos wird Ordnung und Ordnung wechselt ins Chaos.

Im folgenden Video sieht man, wie sich bei einer strömenden Flüssigkeit aus chaotisch ablaufenden Mustern plötzlich geordnete Strukturen bilden.

Und den Wechsel von Chaos und Ordnung kann man auch beim Kochen beobachten..., das mit der Evolution und den Fröschen habe ich nicht so ganz verstanden ...

 Übrigens:
Wer mir bis zum 1.7.2020 einen ähnlichen Film (mit Handy) zusendet (denke an Griesbrei etc...nicht an weitere Tiere...) erhält zwei Essensgutscheine von Betty Baguetti.

Was ist aber nun ein chaotisches System?

Das erkläre ich im nächsten Post, bevor wir uns chaotische komplexe Zahlsysteme ansehen.

Teil 6: Vom Komplexen ins Chaos, Abschnitt 4: Das Feigenbaumdiagramm

Mitchell Feigenbaum (1944 -2019) war ein amerikanischer Physiker, der Pionierarbeit im Bereich Chaos und Fraktale geleistet hat.

In den letzten Posts habt ihr gesehen, und sicher das ein oder andere mal auch  selbst gerechnet, wie man die Folgen von Zahlen x bestimmt, die wir als prozentualen Anteil der Kaninchenpaare an der maximal möglichen Bevölkerung angesehen haben.

Wir haben verschiedene Vermehrungsraten ausprobiert (unsere a Werte) und dabei zeichnet sich die folgende Regel ab (schaut dazu immer mal in dne letzten Post):

a zwischen 0 und 1: 
Die Population stirbt aus. Nach wenigen Jahren ist kein Kaninchen mehr da.

a zwischen 1 und 2: 
Die Population stabilisiert sich zu einer festen Prozentzahl (Grenzwert), die von a                             abhängt:
                                 a - 1/a,

d.h, für a =1 stirbt die Population noch aus, der Grenzwert ist 1 - 1/a = 0.
Aber schon für eine leicht erhöhte Vermehrungsrate von a = 1,1 entsteht der Grenzwert
1,1 - 1/1,1 = 0,191,
d.h. die Population stabilisiert sich auf einen Endwert, der bei 19,1 % der maximal möglichen Populationsgröße liegt.

a zwischen 2 und 3:
Der Endzustand wird abwechselnd von größeren und von kleineren Werten angepeilt, aber erst nach sehr sehr vielen Jahren erreicht.

a zwischen 3 und 3,45:
Nun gibt es zwei mögliche Endzustände, zwischen denen die Population hin- und herwechselt. Dieses Aufteilen sieht wie eine Gabel aus, man nennt das Bifurkation, manchmal irreführend Periodenverdopplung.

a zwischen 3,45 und 3,54: 
Vier mögliche Endzustände wechseln sich ab

Und das geht mit einer immer schnelleren Folge von Verdopplungen weiter, aber:

a größer als 3,57:
Es gibt keine Regelmäßigkeit mehr, die Population verhält sich chaotisch.
Im nächsten Post werden wir klären, was das genau bedeutet.

Schaut nochmal die Bilder vom letzten Post an.
Wenn ich bei diesem chaotischen Fall die Startzahl nur etwas ändere, verläuft die Entwicklung nach wenigen Jahren komplett anders.
Das nennt man die Anfangssensitivität des Chaos. Darauf gehen wir bald ein.

Wir haben also gesehen, für viele a gibt es stabile Endzustände.
Ab a = 3,57 muss man einfach irgendwann die Berechnung abbrechen und den letzten Wert als "End"zustand nehmen.

Wenn man nun alle diese Endzustände gegen das a aufträgt, dann erhält man das weltberühmte Feigenbaumdiagramm. Es ist hier ab a = 2,6 dargestellt.

Das Diagramm hat auch fraktale Strukturen, d.h. es ist aus sich selbst zusammengesetzt. Wenn man hineinzoomt, findet man wieder ein solches Bild:

Wer mit Feigenbaumdiagrammen spielen möchte und auch hineinzoomen möchte, kann das mit der Simualation von Prof. Matzdorf der Uni Kassel sehr gut machen:

Feigenbaumdiagramm Simulation

Mehr im nächsten Post

Teil 6: Vom Komplexen ins Chaos, Abschnitt 3: Material für das Feigenbaumdiagramm

Wir arbeiten mit der folgenden Gleichung:

Wir wollen erst einmal die Vermehrungsrate, das a variieren:
a uist das Verhältnis aus der neuen Anzahl der Kaninchenpaare zur alten Anzahl. a =2 beduetet z.B., das jedes Kaninchenpaar zwei weitere erzeugt.

Alle Berechnungen fangen mit x1 = 0,29 an, d.h. 29% der zur Verfügung stehenden Fläche für Kaninchen sind durch Kaninchenpaare belegt.
Die Kurven (erzeugt mit GeoGebra) geben die Entwicklung der Kaninchenpaare für die ersten 30 Jahre an (n ist die Jahresnummer).

a= 0,44

Die Kaninchenpopulation stirbt schon nach wenigen Jahren aus.

a = 1,0

Früher oder später wird auch diese Population aussterben.

a = 1,5

Recht schnell stellt sich ein Gleichgewicht ein zwischen Neuproduktion vion Kaninchen und Beschränkung des Lebensraumes. Die Population ist stabil.

a = 2,94

Auch hier entsteht ein Gleichgewicht, das aber periodisch nach oben und nach unten abweicht. Etwas zuviel Kaninchen in einem jahr behidnern die Ausbreitung im folgendne Jahr, dadurch fallen Einschränkungne weg und die verbliebenen Paare können den Nachwuchs besser durchbringen. Die Abweichungen werden im Laufe der Zeit immer kleiner.

a= 3,42

Am Anfang sieht es so aus, als gäbe es eine Gleichgewichtspopulation. Dann zeigt sich aber sehr schnell, dass es zwei mögliche Zustände gibt: eine Population mit mehr und eine Population mit weniger Kaninchen. Beide Zustände wechseln sich ab. Das nennt man eine Periodenverdopplung, auch Bifurkation.

a= 3,54

Nun haben sich vier mögliche Populationsgrößen eingestellt, die sich ebenfalls ständig abwechseln.

a = 3,76 (Startwert 0,29)

Man wird hier keinerlei Regelmäßigkeit finden,,,die Anzahl der Kaninchen entwickelt sich chaotisch.
Fängt man statt mit x1 = 0, 29 mit einem nur geringfügig anderen Startwert an (hier x1 = 0,3), so entsteht nach wenigen Jahren eine vollkommen andere Entwicklung:

a = 3,76 (Startwert 0,3)

a = 4,0

Wir sind weiterhin im Chaos.
Ist die Vermehrungsrate über 4,0, so steigt der Wert für xn sehr schnell über 1 an, d.h. die Kaninchenpopulation explodiert.
Beispiel: a =5, x1 = 0,29 ergibt nach 4 Jahren eine Überbelegung von 3625 %...

Im nächsten Post fassen wir zusammen und stellen über die Endzustände der Entwicklung das Feigenbaum-Diagramm zusammen.
Daran erklären wir, was Chaos bedeutet und was ein fraktales Muster ist.

Und dann machen wir das mit komplexen Zahlen...

Teil 6: Vom Komplexen ins Chaos, Abschnitt 2: Logistische Gleichung

Nun wollen wir unser Rechenverfahren leicht abändern.
Zuerst wollen wir jetzt die Werte für xn als prozentuale Anteile auffassen, d.h. x1 = 0,01 bedeutet, dass 1% des zur Verfügung stehenden Raumes für die Kaninchen belegt ist (durch Kanninchen natürlich). dadurch geben wir keine Anzahlen mehr an, sondern  nur noch Prozente.
Ein Zusatzfaktor (1-xn) begrenzt das Wachstum. Kommt xn an die 1, also an 100% ran,  so wird der Begrenzungsfaktor 1-xn kleiner und die nächste Populationsprozentzahl steigt nicht mehr so stark an.
Vereinfacht: Sind zuviel Kaninchen da, begrenzt sich die Population wegen Platz- oder Nahrungsmangel von allein. Unsere Gleichung lautet jetzt:

x(n+1) = a*xn * (1-xn)  = a*xn - a*(xn)².

Ich schreib das auch nochmal in gewohnter Weise auf:

Ich rechne mal ein paar Beispiele durch.
Wir haben a = 2 und x1 = 0,01:

x(n+1)  a*xn    a*xn * (1-xn)
x2         0,02      0,0198
x3         0,04      0,0388
x4         0,08      0,0746
x5         0, 6       0,0138
x6         1,2        0,238

Rechnet mal nach und zeichnet euch das mal auf...auf die x-Achse die Nummer (die Jahreszahl) und auf der y-Achse der Wert für x(n+1).

Und jetzt müsst ihr spielen...
Nehmt mal verschiedene Anfangswerte x1, variiert die Vermehrungszahl a (a =0,2 oder  a=1 oder  a=3 oder  a=3,4 oder a=5....).

Versucht mal Regelmäßigkeiten zu erkennen.

Alles seltsame, das passiert, liegt daran, dass wir jetzt eine nichtlineare Gleichung haben (es steht ein Quadrat oben n der Gleichung).

Die Gleichung heißt auch Verhulst-Gleichung, nach ihrem Entdecker 1845, oder logistische Gleichung.

Und wenn wir statt reellen Zahlen in der nächsten Runde das mit komplexen Zahlen machen, wird es noch interessanter.

wird fortgesetzt...

Lösung

Für die ersten Jahre ergeben sich die folgendne Werte:

n    xn
1     10
2     20
3     40
4     80 usw.
Der Graph sieht wie folgt aus:

Und wie rechnet man die jahre aus?

Zuerst braucht man die Fläche von Australien in m², das sind 7600 000 000 000 m². Das isz usner Wert xn. Unser Wert für x1 ist 1 m².
Damit können wir nun über den Logarithmus den zugehöriogen Wert für n ausrechnen:

Im nächsten Post verhindern wir das...und dann machen wir das ganze mit komplexen Zahlen und dann passieren ganz andere Dinge...

Fehlerkorrektur: Beim ersten Durchrechnen hatte ich 40,5 Jahre raus...heute morgen nicht...habe dne Fehler nicht gefunden, aber ein aufmerksamer Leser: Ich habe vergessen, dass x1 = 10 ist. Wir haben ja mit 10 Paaren angefangen...
wenn man das ein setzt, erhält man die auch zuerst angegebenen 40,5 Jahre.

Teil 6: Vom Komplexen ins Chaos, Abschnitt 1: Von Räubern und Beute

Populationsdynamik

Im ersten Weltkrieg wurde die Fischerei stark eingeschränkt, man beobachtete eine starke Zunahme der Haie.
Seit dieser Zeit beschreibt man die Beziehung zwischen Räubern (Hai) und Beute (Fisch) durch mathematische Gleichungen.
Damit wollen wir uns zuerst beschäftigen, einmal, weil ihr sog. rekursive Formeln kennenlernt und zum anderen, weil wir viele Eigenschaften chaotischer Systeme erkennen können.

Kaninchen in Australien

Manchmal geraten Dinge aus der Kontrolle...ob das die Population der Kaninchen ist, die ohne natürliche Feinde sich nach der   Besiedlung Australiens stark vermehren konnte, der Corona-Virus oder Grippewelle.

Nehmen wir an, im ersten Jahr bringen die Siedler x1 Kaninchenpaare nach Australien. Die vermehren sich innerhalb eines Jahres mit einer  Rate von a.
Dann sind es im zweiten Jahr x2 = a*x1 Kaninchenpaare. Wenn die Vermehrungsrate bleibt, dann kommen wir im dritten Jahr auf x3 = a*x2 = a²*x1 Paare.

Es ist also xn = a^(n-1)* x1 oder aber x(n+1) = a*xn

Ich schreib das mal handschriftlich aus, dann wird die Struktur der Formeln klarer.

Ich denke, es ist klar, wir haben einen Fall von exponentiellem Wachstum vor uns.
Ihr solltet das aber mal selbst berechnen und in einem Graphen zeichnen:

Wir fangen mit 10 Exemplaren an: x1 = 10 und haben eine Vermehrungsrate von 2.
Wie wächst die Population der Kaninchenpaare an?

Und  für Fortgeschrittene: Wenn jedes Kaninchenpaar 1 m² Fläche benötigt, wann ist Australien mit Kaninchen vollständig belegt? Antwort: 40,5 Jahre....(ursprünglicher richtiger Wert

Am Samstag geht es weiter...

spätestens, vielleicht sogar Freitagabend...-bin grad sehr mit Vorbereitungen für dne Neustart beshcäftigt.
Plane als nächstes Itearationen und Fraktale zu posten...

Lösung: Formeln für Sinus und Cosinus

Hier nun die Lösung der letzten Zusatzaufgabe.

Dazu muss man die Darstellung von z + z# und z-z#, also die Summe bzw. Differenz  aus einer komplexen Zahl und ihrem Spiegelbild (komplex konjugierte Zahl) bilden.
Wir haben das hier schon einmal besprochen:

Summe und Differenz

 Bitte beachten: Handschriftlich bezeichne ich z# mit einem Stern oben am z, so wie es üblich ist.

Lösung: irrational und imaginär zusammen wird natürlich

Es ist schon irre, kombiniert man eine Zahl (e) , die man nicht hinschreiben kann (weil sie unendliche viele Stellen hat), mit einer Zahl, die rein imaginär in unserer Einbildung existiert (i), so entsteht eine 1 (bzw. -1)!

Hier die Lösung:

Und noch eine weitere Aufgabe:

y ist natürlich ein Winkel im Bogenmaß.

Teil 5: Die komplexe e-Funktion, Abschnitt 2: das i im Exponenten macht den Kreis...

Die komplexe e-Funktion f(z) = exp(z)

Hier ist wie üblich z = x + iy eine komplexe Zahl.

Wie rechnet man denn exp(z) aus?

Zur Erinnerung exp(x) steht für eˣ.

In der Tat gibt es keine direkte Rechenanweisung für das e-hoch bei einer komplexen Zahl.
Aber wir haben ja gesehen, dass man die e-Funktion als Summe normaler Potenzen schreiben kann und jede Potenz ist eine Multiplikation...und deshalb kann man genau darüber festlegen, wie man exp(z) für eine komplexe Zahl ausrechnet: über die Summe aus Potenzen von z!

Das was für eine reelle Zahl x gilt, gilt genau so für eine komplexe Zahl z!

 Ich muss nur das x durch ein z ersetzen...
Dann habe ich f(z) = exp(z) definiert.

Im letzten Post haben wir gesehen, was exp(x) bedeutet: exponentielles Wachstum...

Ihr werdet staunen, wenn ihr jetzt seht, was exp(z) bedeutet: Einfach nur einmal im Kreis herum, immer wieder...

Kreise haben was mit sinus und cosinus zu tun...
also schreiben wir noch einmal die Summen für sin, cos und exp(x) hin...

Hier habe ich die Fakultäten ausgerechnet (3! = 1*2*3, zur Erinnerung):

Irgendwie hat man das Gefühl, dass die Summen für sin und cos in der für exp(x) drinstecken:
Bei sin kommen nur ungerade Potenzen vor, bei cos nur gerade und bei exp(x) alle...
Aber die Vorzeichen passen nicht!

Ersetzen wir jetzt die reelle Hochzahl x bei exp(x) durch eine rein imaginäre Zahl i*y.

Wenn wir uns daran erinnern, dass i² = -1 ist und somit i³= -i ist etc, dann sind wir mit ein bisschen Umformerei schnell am Ziel:

exp(iy) = cos y +i*sin y   (Eulersche Formel)

Das ist ein Kreis um den Ursprung mit Radius 1! Dabei kann ich y beliebig groß machen, ich komme nicht von diesem Kreis runter...immer im Kreis...

Könnt ihr euch vorstellen, was exp(-iy) bedeutet? Nicht exponentieller Abfall, sondern????

 Übrigens, das was wir hier gerade gemacht haben, hat Leonard Euler (1707-1787) herausgefunden, das ist schon 270 Jahre bekannt...

Und nun können wir auch ganz allgemein die e-Funktion für eine komplexe Zahl z = x + i*y hinschreiben:
 

Das ist ein Kreis mit dem Radius r = |z|.

Ist schon irre, was ein einfaches i im Exponenten aus einem exponentielen Anstieg macht: einen  immer währenden Kreisverkehr...

Das Bild der Funktion f(z) = exp(z) ist also ein Kreis und in diesem Kreis stecken für den Realanteil von z (das x) die cos-Funktion und für den Imaginäranteil von z (dem y) die sin-Funktion...

Sinus und Cosinus zusammengefasst in einer komplexen Funktion..

Manche erahnen jetzt vielleicht schon, warum Physiker/innen und Elektrotechniker/innen die komplexen Zahlen mögen...

dsprelated

Aufgabe: 

Zeige, dass wenn ich die beiden irrationalen Zahlen e und π mit der imaginären Zahl i geschickt kombiniere, entsteht was ganz Einfaches, nämlich - 1 oder +1...

Übrigens, wer sich die ganze Herleitung ausdrucken will:

Ergänzung

Für einige sind vielleicht solche Summenformeln ungewohnt, deshalb führe ich hier mal Rechnungen vor:
Nehmen wir 3,14, das ist ungefähr Pi π, d.h. wir wissen, was bei Sinus und Cosinus rauskommen muss:
sin π = sin 180° = 0
cos π = cos 180° = -1

Nun rechnen wir mit den ersten Summanden  unserer Formeln:

sin x = x/1 - x³/3! + ...
          = 3,14 - 30,96/6 + 305,2/120 = 0,52
Das liegt noch nicht sonderlich dicht an 0, aber der nächste Summand ergibt - 0,6 und schon sind wir bei 0,08...

cos x = 1-x²/2 + ...
         = 1 -4,93 + 4,05
         = 0,12 passt auch noch nicht sehr gut...
der nächste Summand liefert - 1,33 und wir sind bei - 1,21

Man sieht, ein Taschenrechner muss da wesentlich mehr Summenden zusammentragen...

Und zum Schluß die e-Funktion:

Wir setzen x = 1, dann muss e = 2,7 herauskommen...

  e = 1 + 1+1/2+ 1/6 + 1/24 = 2,71...da haben wir schon mit 5 Summanden einen guten Wert für e erhalten...

Teil 5: Die komplexe e-Funktion, Abschnitt 1: e-Funktion im Reellen

Teil 5: Die komplexe e-Funktion

Abschnitt 1: Exponentielles Wachstum und exponentieller Zerfall - die reelle e-Funktion

Leider hat uns die Corona-Pandemie vor Augen geführt, was exponentielles Anwachsen bedeutet. Am Anfang meint man, Wirkungen kaum zu spüren und lange Zeit sieht es so aus, als ändere sich nichts...
Und dann plötzlich geht es los...

Berühmt ist folgendes Beispiel:
Legt man auf das erste Feld eines Schachbrettes ein Reiskorn, und verdoppelt auf dem nächsten Feld immer  die Anzahl, dann kann man mit dem Reis, der auf den ersten 8 Feldern liegt, sich noch nicht einmal satt essen.
Aber die gesamte Weltreisproduktion reicht nicht, um alle 64 Felder des Schachbrettes zu füllen...

Wer sich etwas ausführlicher damit beschäftigen möchte, auch mathematisch, und auf Corona bezogen, dem sei dieses Video empfohlen:

Eine besondere Bedeutung hat die Funktion f(x) = exp (x) = eˣ.

Die Zahl e = 2,78...haben wir am 5.4. schon kennengelernt.

Irrationale Zahlen

Sie ist eine irrationale Zahl, als Basis einer Exponentialfunktion bewirkt sie, dass an jeder Stelle der Funktionswert so groß wie die Ableitung, also die Steigung, ist.

Entsprechend beschreibt exp(-x) einen exponentiellen Abfall.

Ich wiederhole das so ausführlich, weil wir im nächsten Post sehen werden, dass die komplexe e-Funktion wirklich total andere Eigenschaften hat!

Da wächst und fällt nichts mehr, da kreist es nur noch...

Um das nachvollziehen zu können, müsst ihr mir das Folgende noch abnehmen:

Darstellung der Funktionen durch eine Summe:

Alle in der Schule vorkommenden (d.-h. nicht bösartigen)  Funktionen kann man auch über eine sogenannte Reihenentwicklung ausrechnen, d.h. über eine Summe:

Sinus-Funktion:

Der erste Teil ist die abgekürzte Summenschreibweise, aber den zweiten Teil sollten alle verstehen:
Wenn ich den Sinus einer Zahl x (im Bogenmaß) berechnen will, muss ich abwechselnd alle ungeraden Exponenten dieser Zahl addieren. Dabei muss ich noch durch die Fakultät des Exponenten teilen. Die Fakultät ist ein Produkt und wird mit ! markiert:
3! bedeutet 1*2*3, 5! = 1*2*3*4*5 usw.

So etwas gibt es auch für die cosinus-Funktion:

Hier sind es die geraden Exponenten, die man nehmen muss.

Ein Taschenrechner kann übrigens nur addieren  und multiplizieren und er berechnet sin und cos über diese Summen. Man kann nach wenigen Summanden abbrechen und erhält ausreichend gute Werte.

Und nun das  Gleiche für die Exponentialfunktion:

Hier wird nur addiert...
Diese drei Reihen sehen ähnlich aus (das liegt daran, dass sie alles sog. Potenzreihen sind), aber ansonsten haben sie nichts miteinander zu tun...

Das wird sich ändern, wenn wir im nächsten Post die imaginäre Einheit i da rein schreiben...

Dann sind wir bei der sicher erstaunlichsten Form der Darstellung komplexer Zahlen, können seltsame Zusammenhänge erkunden und verstehen endlich, was ein Kreis ist...

Wann geht es weiter?

Bestimmt am Sonntag, denke, da sind auch die Bildprobleme gelöst...aber ich will bis Sonntagmittag abwarten, damit ich nicht vergeblich was hochlade, was dann gleich weg ist...
Als nächstes kümmern wir uns um Kreise und die letzte Darstellung von komoplexen zahlen...

Achtung! Probleme mit Blogspot

...viele Bilder werden zur Zeit nach Neustart nicht hochgeladen,  seit 2 Stunden ist google am fixen, denke , das Problem ist bald gelöst...ansonsten lade ich am Sonntag die letzten Bilder neu hoch,
da das viel Arbeit macht, würde ich gerne warten....

Bitte am Sonntag Rückmeldung geben wo noch Bilder fehlen



Aktualisierung: Das Problem ist weltweit aufgetreten. Google muss alle Bilddatein restaurierenn...das dauert. Aber im Google Bildarchiv sind alle Bilder der Blogs in der hochgeladenen Reihenfolge  erhalten. Ich habe begonnen, die letzten Posts zu restaurieren.
So 10.00 Uhr: Bis einschl. 7.4.  müsste wieder vollständig sein (vom aktuiellen rückwärts, die früheren kommen später dran)..
Für den Rest warte ich noch ab. Zum Glück fehlen nicht alle Bilder. Wenn jemand drignend ein bestimtmes Bild braucht, bitte per Mial melden oder in discort...ich ersetze es dann gleich!

Teil 4: Polardarstellung komplexer Zahlen, Abschnitt 3: Wir wurzeln, Teil 3

Wir wurzeln immer weiter...

Hier erst einmal die Lösungen:

Aufgabe 1: Löse z³ = i

Das ist eine Gleichung dritten Grades. Die muss genau drei Lösungen haben...

Schritt 1: 
Schreibe das i in Polardarstellung, aber lasse alle Möglichkeiten für die Winkel zu, also addiere k*360° zu dem Winkel (für i ist das 90° + k*360°).

Schritt 2: 
Ziehe die dritte Wurzel, in dem Du die dritte Wurzel aus dem Betrag (Radius, Vorfaktor) ziehst und den Winkel unter dem cos und dem sin durch 3 teilst (Moivresche Formel).

Schritt 3: 
Gehe von k = 0 aus und bestimme so lange Lösungen, bis sich alles wiederholt...
Bei der dritten Wurzel geht es mit k=0, k=1 und k=2

Schritt 4: 
Jetzt kannst Du schon zeichnen und die Werte abschätzen.

Schritt 5: 
Mit einem Taschenrechner kannst Du Näherungswerte bestimmen.

Ich hab das mal für euch gerechnet:

Eine mögliche Lösung der Gleichung ist -i, also ∛i = -i als ein Wert...
das kann man leicht überprüfen: (i*i)+i = -1*i = - i
Die anderen beiden Lösungen sind komplexe Zahlen, wem langweilig ist, der kann das ja auch mal überprüfen...

Aufgabe 2: Löse z³ = 8

Das ist doch klar...z = 2, weil  ∛8 = 2...
ja, das ist eine der drei Lösungen, denn 2*2*2 = 8
aber es gibt noch zwei weitere Lösungen, das sind aber komplexe Zahlen, da ist die Überprüfung schwieriger als das Ausrechnen:

Wir haben jetzt wirklich gelernt, wie man alle (!!) Wurzeln einer Zahl bestimmt.

Leider müssen wir in Kauf nehmen, dass wir die Lösungen unserer Gleichungen nicht mehr nach der Größe ordnen können...

Und schaut euch mal meine Skizzen an:

Die Lösungen bilden regelmäßige n-Ecke...

Ich finde das faszinierend... Gauß wohl auch, er hat auch gezeigt, dass man das 17-Eck nur mit Zirkel und Lineal konstruieren kann...damals war er 18 jahre alt.

1894 hat Gustav Hermes eine 200 Seiten umfassende Konstruktionsvorschrift für ein 65537 -Eck abgeliefert.
Das war noch Einsatz!

Man kann inzwischen genau beweisen für welche Eckenzahl man die Konstruktion mikt Zirkel und Lineal machen kann.
Früher habe ich in der Klasse 8 das noch für Dreiecke unterrichtet.
Macht man das heute immer noch?

Das Bild hier wird euch jetzt bestimmt was sagen:

Da wurde einmal die zweite, einmal die dritte und einmal die vierte Wurzel aus einer Zahl bestimmt.

Und hier nochmal eine Darstellung mit Geogebra:
Die Zahl z, aus der die dritte Wurzel gezogen wird, ist in grün dargestellt, die drei Wurzeln in rot.

Die besondere Schreibweise mit der e-Funktion lernen wir noch kennen.

Teil 4: Polardarstellung komplexer Zahlen, Abschnitt 3: Wir wurzeln, Teil 2

Wir wurzeln weiter...

Hier lernt ihr, wie man bei komplexen Zahlen mehrere Werte (komplexe Werte) für Wurzeln erhaltet.

Bei der zweiten Wurzel gibt es zwei Werte, bei der dritten immer (!!!) drei Werte, bei der vierten Wurzel immer vier Werte...
Besser kann es nicht kommen! Da freut sich das Mathematikerinnenherz!

Und zeichnet dann diese Werte mal in das Koordinatensystem ein...alles schön regelmäßig und symmetrisch!

Ich habe euch das erst einmal für √i aufgeschrieben.

Was ungewöhnlich ist...wir dürfen keinen bestimmten Winkel mehr nehmen, sondern immer beliebig viele volle Umdrehungen links- oder rechtsherum zusätzlich. Das drücken wir durch k*360° aus, die wir zuaddieren (oder effektiv abziehen, wenn k negativ ist). Nur für k=0 erhält man den sagen wir "üblichen" Wert...

 Und nun das Ganze für √2:

Ich hab dann am Ende das für die Lösung von Gleichungen z² = i und z² = 2 umgeschrieben.
Man erhält dann jeweils zwei Lösungen.
Macht mal die Probe...setzt für z mal jede der beiden Lösungen ein und rechnet das nach...es kommt wirklich hin! Ich habe das für z² = i angefangen, aber dann abgebrochen...sollt ihr mal selbst weitermachen...

So und nun kommen wir zum nächnsten Schritt:

Macht das jetzt mal für die dritten Wurzeln! Also bestimmt die Lösungen für die folgenden Gleichungen:

   z³ = i sowie z³ = 8

Denkt dran: dritte Wurzel bedeutet hoch 1/3!
Haltet euch ruhig an die Vorlagen oben und zeichnet mal die jeweils drei Lösungen in das Koordinatensystem ein!

Teil 4: Polardarstellung komplexer Zahlen, Abschnitt 3: Wir wurzeln, Teil 1

Wir haben uns ja die komplexen Zahlen ausgedacht, um Gleichungen der Form z² = -1 lösen zu können und haben dann die neue Zahl i = √(-1) eingeführt.

Nun müssen wir aber zeigen, dass unsere neuen Zahlen auch wirklich dafür geeigent sind...
also wurzeln wir mal drauf los...
Ihr werdet manche Überraschung erleben...und das gipfelt in der Doktorarbeit von Herrn Gauß...

Wir fangen  mit zwei  einfachen Beispielen an, √i und √2 und werden  merken, dass wir bei der ersten Rechnung was wichtiges vergessen  haben...nämlich dass man beliebig oft im Kreis gehen kann ohne an ein Ende zu kommen...

Ihr braucht nun die Polarschreibweise und die Moivresche Formel.

Hier meine Notizen dazu:

Lösungen der Aufgaben

Teil 4: Polardarstellung komplexer Zahlen, Abschnitt 2: Multiplizieren und Dividieren

Rechnen in der Polardarstellung

Wir legen erst einmal die beiden komplexen Zahlen z1 = r1* (cos φ1 + i* sin φ2)
und z2 = r2 * (cos φ2 + i* sin φ2 ) fest mit den Beträgen r1 und r2 und den Winkeln φ1 und φ2 fest.

Wenn man addieren will, ist es am einfachsten in die bekannte Form z = x + i*y  umzurechnen. Wir wollen sie ab jetzt die arithmetische Form nennen.

Die Polardarstellung ist dagegen besonders gut für die Multiplikation und Division komplexer Zahlen:

Die Formel wollen wir nicht herleiten, das ist im Prinzip aber nicht so schwer. Man muss einfach eine Summe aus Sinüssen und Cosinüssen vereinfachen. Dazu gibt es die Additionstheoreme, die man früher in der Schule herleiten und können musste. Heute  werden  sie oft in der Schule noch nicht mal erwähnt.

Ich gebe die Endformeln an:

z1 * z2 = r1*r2 * [cos (φ1 + φ2) + i * sin (φ1 + φ2)]
Multiplizieren: Beträge  multiplizieren, Winkel addieren

 z1 / z2 = r1/r2 * [cos (φ1 - φ2) + i * sin (φ1 - φ2)]
Dividieren: Beträge dividieren, Winkel subtrahieren 

Man könnte auch so sagen:
Der Produktzeiger ist weitergedreht und gestreckt worden, der Quotientenzeiger zurückgedreht und gestaucht worden.
Das haben wir schon kennengelernt. Hier noch mal das Bild dazu:

matheistkeinarschloch

Und so sieht das in der Polardarstellung aus:
Winkel addieren, Zeigerlängen multiplizieren und schon hat man den Produktzeiger.

Am besten ihr übt das mal:

Aufgabe 1:
Zeichnet die Zeiger zu z1 = 2 * (cos 30° + i * sin 30°)
                         und zu z2 =  3 * (cos 45° + i* sin 45°)
in ein Koordinatensystem

Dann bildet z1*z2 und z1/z2 und zeichnet die neuen Zeiger.
Produkt und Quotient könnt ihr eigentlich direkt aus den Angaben für z1 und z2 ablesen...ihr müsst nurn noch zeichnen...

Irre: Ihr könnt jetzt komplexe Zahlen im Kopf multiplizieren und dividieren!  😎

Zum Schluss noch eine ganz wichtige Formel, die uns bald helfen wird, Wurzeln konkret hinzuschreiben:

Hier wird einfach zⁿ, die n-te Potenz gebildet.

Ihr wisst, was das bedeutet: z*z*z*z*z... (n-mal)...jedesmal wird das r mit sich multipliziert und der Winkel auf sich selbst addiert...
und schon ist die berühmte Formel von Moivre fertig:

zⁿ = rⁿ * [cos(n*φ) + i * sin(n*φ)]


Ihr könnt jetzt übrigens auch komplexe Zahlen im Kopf potenzieren:

Macht das mal...

Aufgabe 2:
Bildet z² und z³ sowie z⁴ zu z = 3 * (cos 80° + i*sin 80°).
Was macht die Zeigerspitze beim Potenzieren?


Wer potenzieren kann, kann auch wurzeln,...und das erkläre ich euch im nächsten Post.
Dann lernen wir auch Vielecke zu zeichnen...

 Im übernächsten  Post erkläre ich dann die häufigste Schreibweise für komplexe Zahlen, die ein Herr Euler gefunden hat. Und mit der kann man dann richtig viel machen...sogar Kreise zeichnen....

Ach, und falls irgendjemand die beiden genannten Formeln herleiten will, hier die Additionstheoreme:

Lösung der Aufgaben oder wie oft kann man die Erde umkreisen bevor man an ein Ende kommt?

a) Gib alle reellen Zahlen in der Polardarstellung an.

r ist beliebig, eben jede reelle Zahl, aber als Winkel können nur 0° (positive reele Zahlen) oder 180° (negative reelle Zahlen vorkommen. Allerdings, wer sagt denn, das man nur einmal herum darf? Auch 350° bzw. 540° bzw.720° produzieren reelle Zahlen:
 Relle Zahlen = z*[cos (0° + k*180°) + i*sin (0° + k*180°)],
    dabei ist z eine reine reelle Zahl und k ist eine beliebige ganze Zahl

b) Welcher Winkel gehört zu den imaginären Zahlen?
Nun: 90° oder 270° oder jeweils immer 180° dazu zählen oder abziehen....
also: 90° + k*180°, k ist eine beliebige ganze Zahl

c) Warum gibt es keine eindeutige Antwort auf diese Fragen?
weil man beliebig oft um Kreise herumlaufen kann, man kommt nie an ein Ende...

d) Wie lautet die Polardarstellung von komplexen Zahlen, die auf der Hauptdiagonalen des Koordinatensystems liegen?
Hier muss man von einem Winkel von 45°, 225°, 405° ....ausgehen und man kann jeden beliebigen Abstand nehmen:
  r*[cos (45° + k*180°) + i*sin(45° + k*180°)]

e) Wie lauten die Polardarstellungen der Zahlen, die auf einem Kreis mit dem Radius 5 um den Ursprung liegen?
Hier muss man r= 5 nehmen und den Winkel beliebig lassen:

  r*(cos φ + i*sin φ )

f) Rechne z = 3 + 4i in Polardarstellung um, ebenso z = 3 -4i und z = -3-4i
Ich gebe erst die Formeln an, mit denen man arbeiten muss:

Den Winkel  φ erhält man über das Tangens-Verhältnis: tan φ = Im/Re = y/x, den  Abstand r erhält man über den Pythagoras: r² = x² + y² und dann die Wurzel ziehen.

Da es beim Quadrieren nicht nauf die Vorzeichen ankommt, erhält man für alle drei Fälle r = 5! Die Punkte liegen also alle auf einem Kreis mit dem Radius 5 um den Ursprung.

Um das Ergebnis, welches der Taschenrechner ausspuckt (normalerweise nur Winkel zwischen -90° und + 90°)  richtig zu interpretieren, überlegen wir erst, in welchem Quadrant der Punkt liegt.
Achtung: Man muss die Umkehrfunktion vom tan drücken, invtan oder wie auch immer bezeichnet...und der Taschenrechner sollte auf degree stehen....

x       y    Quadrant     tan φ     φ
3       4           I              4/3       53°
3      -4          IV           -4/3       -53° oder 360-53 = 307°
-3     -4          III            4/3       53+180 = 233°
Läge der Punkt in Quadrant II müsste man 180 - 53 = 127° rechnen.
Ja und dann müssen wir noch alle anderen Winkel zulassen, die durch Addition oder Subtraktion von Vielfachen von 360° entstehen.

Meistens begnügt man sich aber ohne diese zusätzlichen Angaben von unendlich vielen Winkeln und spricht dann vom Hauptwert der Lösung.

Das waren Übungsaufgaben, die eigentlich viel Lerninhalt hatten. Also nicht verzagen, wenn man die nicht alleine lösen konnte.

spektrum

Hinweis: Rechts in der Computerversion (unter den Zusatzseiten) gibt es zwei Hilfen zu trigonometrischen Funktionen wie sin und cos...)

Teil 4: Polardarstellung komplexer Zahlen, Abschnitt 1: Einführung

Einführung der Polardarstellung einer komplexen Zahl

Komplexe Zahlen haben wir bisher als Punkt in der Gaußschen Zahlenebene dargestellt. Die erste Koordinate war der Realteil, die zweite der Imaginärteil: z = (Re z, Im z).
Oder man gibt komplexe Zahlen als Summe aus Real- und Imaginärteil an: z = Re z + i* Im  z

Hauptsache, das Rechnen klappt wie gewohnt...
Und das tut es, haben wir ja überprüft.
Wenn wir jetzt komplexe Zahlen auf andere Art notieren, muss die Rechnerei weiterhin so wie bisher gehen...

Nun kann man aber komplexe Zahlen auch durch ihren Abstand zum Ursprung (Betrag |z| oder auch mit r bezeichnet) und durch den Winkel, den die Verbindungslinie z zum Ursprung mit der reellen Achse einnimmt (mit φ oder α bezeichnet) angeben.

Falls es jemand kennt: Das ist wie bei Polarkoordinaten!

lpunikgoettingen

Wie können wir nun den Realteil a und den Imaginäranteil b über r=|z| und den Winkel φ ausdrücken?

Dazu muss man sich das rechtwinklige Dreieck aus a, b und r ansehen.
b ist die Gegenkathete zum Winkel φ und a die Ankathete. Die Strecke r = |z| liegt dem rechten Winkel gegenüber, das ist die Hypotenuse im rechtwinkligen Dreieck.
(Man erinnere sich: a² + b² = c², äh r²)
Damit kann man die Winkelfunktionen sin φ und cos φ aufstellen.

Wer sich damit nicht auskennt:
Im Laufe des Tages mache ich eine Zusatzinformationsseite dazu ( siehe rechts).
Ansonsten:
Der Sinus eines Winkels ist das Verhältnis aus Gegenkathete zur Hypotenuse im rechtwinkligen Dreieck, der Cosinus des Winkels das Verhältnis aus Ankathete zur Hypotenuse.
Ein Taschenrechner kennt diese Zahlen...und kann damit rechnen...sogar, wenn die Winkel über 90° weitergehen...beliebig weit...

Für uns gilt:
cos φ = Ankathete/Hypotenuse = a/r, also a = r* cos φ
und
sin φ = Gegenkathede/Hypotenuse = b/r, also b = r * sin φ

Das setzen wir nun  in z = a + ib ein und erhalten die Polardarstellung der komplexen Zahl:

z = r*cos φ+ i*r* sin φ  = r *(cos φ+ i * sin φ).

ruhrunibochum

wikimathe

Das lässt sich auch leicht auf die konjugiert komplexe Zahl übertragen:

 Welche komplexe Zahl ist hier gemeint:

Antwort: z = (0,74, 0,67) = 0,74 + i*0,67 = 1* (cos 41,9° + i* sin 41,9°) oder (#1, 41,9°) in der Polardarstellung.

Umkehrung der Rechnungen:

Wir sollten noch kurz angeben, wie man aus der normalen Darstellung z = x + i*y  die Werte für r und φ erhält:

Bestimmung des Abstandes r ( = Bestimmung des Betrages, hatten wir also schon):

 r² =  x² + y², ist wieder der olle Grieche...P.

Bestimmung des Winkels:

Für den Winkel muss man die Winkelfunktion Tangens benutzen:

tan  φ = Gegenkathede/Ankathete = y/x

Der Taschenrechner kann da nicht alle möglichen Lagen des Punktes berücksichtigen. Am besten überlegt man sich in welchem Quadranten die komplexe Zahl liegt und benutzt den vom Taschenrechner ausgegebenen Winkel um daraus einen Winkel zwischen 90° und 180° oder 180° und 270° oder 270° und 360° auszurechnen.


Übung:
a) Gib alle reellen Zahlen in der Polardarstellung an.
b) Welcher Winkel gehört zu den imaginären Zahlen?
c) Warum gibt es keine eindeutige Antwort auf diese Fragen?
d) Wie lautet die Polardarstellung von komplexen Zahlen, die auf der Hauptdiagonalen des Koordinatensystems liegen?
e) Wie lauten die Polardarstellungen der Zahlen, die auf einem Kreis mit dem Radius 5 um den Ursprung liegen?
f) Rechne z = 3 + 4i in Polardarstellung um, ebenso z = 3 -4i und z = -3-4i..

Die Lösungen kommen bald, aber sucht es erst einmal selbst.

Und danach lernen wir wieder Adidieren und Multipülizieren in der Polardarstellung...und werden merken, dass man jetzt diese Rechenarten noch leichter veranschaulichen kann.

Und nicht vergessen: In SFNonline kann man Fragen stellen...

Videos:
Sehr schön ruhig und sachlich erklärt das die Dame hier:

Eine gute ausführliche Darstellung, aber auch weiterführend, ist hier zu sehen: