Komplexe Zahlen haben wir bisher als Punkt in der Gaußschen Zahlenebene dargestellt. Die erste Koordinate war der Realteil, die zweite der Imaginärteil: z = (Re z, Im z).
Oder man gibt komplexe Zahlen als Summe aus Real- und Imaginärteil an: z = Re z + i* Im z
Hauptsache, das Rechnen klappt wie gewohnt...
Und das tut es, haben wir ja überprüft.
Wenn wir jetzt komplexe Zahlen auf andere Art notieren, muss die Rechnerei weiterhin so wie bisher gehen...
Nun kann man aber komplexe Zahlen auch durch ihren Abstand zum Ursprung (Betrag |z| oder auch mit r bezeichnet) und durch den Winkel, den die Verbindungslinie z zum Ursprung mit der reellen Achse einnimmt (mit φ oder α bezeichnet) angeben.
Falls es jemand kennt: Das ist wie bei Polarkoordinaten!
 |
| lpunikgoettingen |
Dazu muss man sich das rechtwinklige Dreieck aus a, b und r ansehen.
b ist die Gegenkathete zum Winkel φ und a die Ankathete. Die Strecke r = |z| liegt dem rechten Winkel gegenüber, das ist die Hypotenuse im rechtwinkligen Dreieck.
(Man erinnere sich: a² + b² =
Damit kann man die Winkelfunktionen sin φ und cos φ aufstellen.
Wer sich damit nicht auskennt:
Im Laufe des Tages mache ich eine Zusatzinformationsseite dazu ( siehe rechts).
Ansonsten:
Der Sinus eines Winkels ist das Verhältnis aus Gegenkathete zur Hypotenuse im rechtwinkligen Dreieck, der Cosinus des Winkels das Verhältnis aus Ankathete zur Hypotenuse.
Ein Taschenrechner kennt diese Zahlen...und kann damit rechnen...sogar, wenn die Winkel über 90° weitergehen...beliebig weit...
Für uns gilt:
cos φ = Ankathete/Hypotenuse = a/r, also a = r* cos φ
und
sin φ = Gegenkathede/Hypotenuse = b/r, also b = r * sin φ
Das setzen wir nun in z = a + ib ein und erhalten die Polardarstellung der komplexen Zahl:
z = r*cos φ+ i*r* sin φ = r *(cos φ+ i * sin φ).
 |
| ruhrunibochum |
 | |
| wikimathe |
Das lässt sich auch leicht auf die konjugiert komplexe Zahl übertragen:
Welche komplexe Zahl ist hier gemeint:
Antwort: z = (0,74, 0,67) = 0,74 + i*0,67 = 1* (cos 41,9° + i* sin 41,9°) oder (#1, 41,9°) in der Polardarstellung.
Umkehrung der Rechnungen:
Wir sollten noch kurz angeben, wie man aus der normalen Darstellung z = x + i*y die Werte für r und φ erhält:
Bestimmung des Abstandes r ( = Bestimmung des Betrages, hatten wir also schon):
r² = x² + y², ist wieder der olle Grieche...P.
Bestimmung des Winkels:
Für den Winkel muss man die Winkelfunktion Tangens benutzen:
tan φ = Gegenkathede/Ankathete = y/x
Der Taschenrechner kann da nicht alle möglichen Lagen des Punktes berücksichtigen. Am besten überlegt man sich in welchem Quadranten die komplexe Zahl liegt und benutzt den vom Taschenrechner ausgegebenen Winkel um daraus einen Winkel zwischen 90° und 180° oder 180° und 270° oder 270° und 360° auszurechnen.
Übung:
a) Gib alle reellen Zahlen in der Polardarstellung an.
b) Welcher Winkel gehört zu den imaginären Zahlen?
c) Warum gibt es keine eindeutige Antwort auf diese Fragen?
d) Wie lautet die Polardarstellung von komplexen Zahlen, die auf der Hauptdiagonalen des Koordinatensystems liegen?
e) Wie lauten die Polardarstellungen der Zahlen, die auf einem Kreis mit dem Radius 5 um den Ursprung liegen?
f) Rechne z = 3 + 4i in Polardarstellung um, ebenso z = 3 -4i und z = -3-4i..
Die Lösungen kommen bald, aber sucht es erst einmal selbst.
Und danach lernen wir wieder Adidieren und Multipülizieren in der Polardarstellung...und werden merken, dass man jetzt diese Rechenarten noch leichter veranschaulichen kann.
Und nicht vergessen: In SFNonline kann man Fragen stellen...
Videos:
Sehr schön ruhig und sachlich erklärt das die Dame hier:
Eine gute ausführliche Darstellung, aber auch weiterführend, ist hier zu sehen:
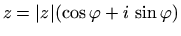


Keine Kommentare:
Kommentar veröffentlichen