Teil 10: Wenn Strom komplex wird, wird alles leichter...III: Drehende Zeiger

Bevor wir zu komplexen Widerständen kommen, möchte ich euch erst eine Methode vorstellen, mit der man die Kurven für I(t) und U(t) erzeugen kann:

Dazu müssen wir aus der Mathematik übernehmen, dass sich drehende Zeiger Sinus-Kurven erzeugen.

Man sagt in der Fachsprache: Die Projektion einer Kreisbewegung ist eine (harmonische) Schwingung.

In diesem Bild zu einer Federschwingung wird klar, was damit gemeint ist:

de scio de

Wenn das Federpendel schwingt, kann man den Zeiger links im Bild sich immer so schnell drehen lassen (gegen den Uhrzeigersinn) , dass seine Spitze immer auf der Höhe der Pendelmasse ist. Trägt man dann den Abstand der Zeigerspitze von der Nulllage gegen die Zeit auf, so erhält man die typische Schwingungskurve ganz rechts.

Das haben wir auf den Infoseiten ja schon zusammengestellt:

Einheitskreis und Sinus

Die Zeigerlänge ist dabei die Amplitude der Schwingung, das wäre dann auch der Kreisradius.

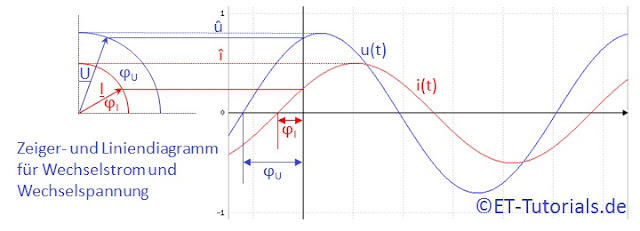
Bei Wechselstrom interessieren uns zwei Schwingungen gleichzeitig, die des Stromes und die der Spannung...
Was machen wir? Wir nehmen zwei Zeiger...und drehen sie mit der gleichen Geschwindigkeit.

Das ist im nächsten Bild dargestellt:

Hier ist für den Winkel zwischen den Zeigern für Spannung und Stromstärke ein beliebiger Wert angenommen worden.

Das ist bei Spule und Kondensator einfacher (das steht in den letzten Posts):

Kondensator: Die Stromstärke eilt der Spannung immer um 90° voraus. Der Winkel zwischen den Zeigern für Spannung und Stromstärke am Kondensator muss also 90° sein.

Spule: Hier eilt die Spannung der Stromstärke um 90° voraus. Anders ausgedrückt: Die Stromstärke hinkt der Spannung um 90° hinterher. Die beiden Zeiger für Spannung und Stromstärke haben auch einen 90° - Winkel dazwischen, nur in der anderen Richtung als beim Kondensator gedreht.

Und wie ist es beim ohmschen Widerstand?
Da sind Spannung und  Stromstärke gleichphasig, also liegen die Zeiger aufeinander!.

Am einfachsten verstehen wir die idee, wenn wir eine Riehenschaltung von Spule, Kondensator und ohmschen Widerstand betrachten.
Diese Schaltung spielt in der Wechselstromtechnik als Siebkette eine große Rolle. Das werden wir hier aber nicht verfolgen.

schule-bw

Durch alle drei Bauteile fließt der gleiche Strom, es gibt also einen einzigen Zeiger für I(t). Den legen wir auf die waagerechte Achse.
Der Zeiger für die Spannung am ohmschen Widerstand muss dann auczh, mit anderer Länge, dort liegen.

Da wir gegen den Uhrzeigersinn drehen wollen (ist so verabredetz), liegt der Zeiger für die Spannung am Kondensator dann um 90° verdreht nach unten. Nur so ist I vor U!
Und der Zeiger für die Spannung an der Spule eilt ja I(t) voraus, er liegt um 90° verdreht senkrecht nach oben.

 

Nun können wir aus den drei Einzelspannungen die Gesamtspannung ausrechnen. Das kann jeder ja mal probieren, mit Hilfe des ollen Griechen...

Und wer kann den Gesamtwiderstand der Schaltung angeben?

Damit machen wir im nächsten Post weiter.

Ich denke, einige ahnen schon, wie wir da mit komplexen Zahlen weitermachen können...Ich muss eigentlich nur noch Real und Im an die Achsen schreiben....

Intermezzo: Experimente

Ja, wir machen Mathematik...aber trotzdem können physikalische Experimente manchmal Dinge veranschaulichen.
Ich habe hier zwei Versuche gefilmt, bei denen man die Phasenverschiebung zwischen Strom und Spannung an Spule und Kondensator durch einen Trick am Oszilloskop sichtbar machen kann.
Zum Trick: Oszilloskope können nur Spannungen messen, keine Ströme. Deshalb habe ich einen kleinen Widerstand in Reihe geschaltet. Die Spannung, die an ihm abfällt (und die das Oszilloskop messen kann) ist proportional zum Strom, der durch den Widerstand fließt.