Am ersten Samstag der Sommerferien findet wieder ein Ferienworkshop für alle besonders an Mathematik Interessierte statt:
Warum rechnet man in der Quantenmechanik mit komplexen Zahlen?
Sa, 4.7., 14-17 Uhr
Teilnahme nur nach Voranmeldung unter info@sfn-kassel.de
Das Wissen über komplexe Zahlen sollte man sich vorher über unseren Online-Workshop angeeignet haben
https://sfnkomplexezahlen.blogspot.com/
Das notwendige Wissen über quantenmechanische komplexe Wellen erwirbt man im Workshop.
Komplexe Zahlen, Elektrotechnik und Fraktale
Wegen der Corona-Pandemie ist das SFN geschlossen. Der Ferienworkshop Mathematik findet deshalb als Blog statt. Austausch und Diskussion in SFN-Online https://discord.gg/eh6eP6E
Ziel des Workshops
Was sind komplexe Zahlen?
Einführung in das Rechnen mit komplexen Zahlen
Komplexe Zahlen sind wie Vektoren sind aber keine Vektoren
Warum es Wurzeln aus negativen Zahlen gibt
Exponentialfunktion liefert Kreise
Einfache Beschreibung von Schwingungen durch komplexe Zahlen
Wechselstromwiderstände lassen sich durch komplexe Zahlen zusammenfassen
Erzeugung von fraktalen Mustern durch einfach Gleichungen
....
Samstag, 30. Mai 2020
Samstag, 23. Mai 2020
Inhaltsverzeichnis
Ich hoffe, dieser reine Mathe-Blog hat etwas Spaß gemacht.
Wer mehr lernen möchte: Ich habe noch einen Blogs über Wechselstromtechnik und elektromagnetische Schwingungen, IR-Astronomie und im Astronomie-Blog sind oft Postserien über Elementarteilchen, Quanten und Kosmologie.
Ich plane einen neuen Blog über Schall und Dopplereffekt. Ab und an mal hier reinsehen, ich werde ihn hier ankündigen.
Inhaltsverzeichnis:
0. Einführung
1. Wie man sich neue Zahlen bastelt
1.1 Das Ausgangsmaterial: natürliche Zahlen
1.2 Paare statt Zahlen
1.3 Rechnen mit Paaren
1.4 Warum Mathematiker die ganzen Zahlen erfunden haben
1.5 Brüche bilden rationale Zahlen
1.6 Rational sein ist nicht alles
1.7 Irrational
2. Vom Zählen und Ordnung schaffen
2.1 Doppelt soviel ist gleich viel?
2.2 Weniger ist mehr?
2.3 Fast überall geht es ordentlich zu
3. Einführen von komplexen Zahlen
3.1 Einleitung
3.2 Paarbildung
3.3 Übugnen und Lösungen
3.4 Richtungszuweisung und Addition
3.5 Übungen
3.6 Multiplikation und konjugiert kompelxe Zahlen
3.7 Division
3.8 Aufgaben und Lösungen
3.9 Der Kehrwert von i
3.10 Über die verlorene Ordnung
3.11 Zwei wichtige Gleichungen
4. Polardarstellung komplexer Zahlen
4.1 Einführung, Aufgaben und Lösungen
4.2 Multiplikation und Division
4.3 Lösungen
4.4 Wir wurzeln
4.4.1 √i und √8
4.4.2 z³ = i
4.4.3 z³ = 8
5. Die komplexe Exponentialfunktion
5.1. Die e-Funktion im Reellen
5.2 Exponentielles Wachstum
5.3 Das i im Exponenten macht den Kreis
5.4 Irrational und Imaginär: zusammen wird es natürlich
5.5. Formelön für Sinus und Cosinus
6. Vom Komplexen ins Chaos
6.1 Von Räubern und beute
6.2 Die logistische Gleichung
6.3 Material für ein Feigenbaumdiagramm
6.4 Das Feigenbaumdiagramm
6.5 Das Chaos im Feigenbaumdiagramm
6.6 Was ist Chaos?
7. Fraktale
7.1 Juliamengen
7.2 Apfelmännchen
7.3 Apfelmännchen und Feigenbaumdiagramm
7.4 Video
8. Hyperkomplexe Zahlen
Einschub: Aus Imaginär wird reell
9. Komplexe Funktionen
10. Wenn Strom komplex wird, wird alles leichter...
10.1 Der Kondensator
10.2 Die Spule
Zugabe: Experimente
10.3 Drehende Zeiger
10.4 Komplexe Widerstände
10.5. Vertiefungen
10.6 Wirk, Blind und Schein
10.7 Beispiel: Berechnung einer Brückenschaltung
Inhaltsverzeichnis
Zusatzseiten:
I. Überblick über Zahlsysteme
II. Rechenregel
III. Körperaxiome
IV. Ordnungsrelationen
V. Sinus und Cosinus
VI. Bogenmaß statt Winkel
VII. Lineare Funktionen
Wer mehr lernen möchte: Ich habe noch einen Blogs über Wechselstromtechnik und elektromagnetische Schwingungen, IR-Astronomie und im Astronomie-Blog sind oft Postserien über Elementarteilchen, Quanten und Kosmologie.
Ich plane einen neuen Blog über Schall und Dopplereffekt. Ab und an mal hier reinsehen, ich werde ihn hier ankündigen.
Inhaltsverzeichnis:
0. Einführung
1. Wie man sich neue Zahlen bastelt
1.1 Das Ausgangsmaterial: natürliche Zahlen
1.2 Paare statt Zahlen
1.3 Rechnen mit Paaren
1.4 Warum Mathematiker die ganzen Zahlen erfunden haben
1.5 Brüche bilden rationale Zahlen
1.6 Rational sein ist nicht alles
1.7 Irrational
2. Vom Zählen und Ordnung schaffen
2.1 Doppelt soviel ist gleich viel?
2.2 Weniger ist mehr?
2.3 Fast überall geht es ordentlich zu
3. Einführen von komplexen Zahlen
3.1 Einleitung
3.2 Paarbildung
3.3 Übugnen und Lösungen
3.4 Richtungszuweisung und Addition
3.5 Übungen
3.6 Multiplikation und konjugiert kompelxe Zahlen
3.7 Division
3.8 Aufgaben und Lösungen
3.9 Der Kehrwert von i
3.10 Über die verlorene Ordnung
3.11 Zwei wichtige Gleichungen
4. Polardarstellung komplexer Zahlen
4.1 Einführung, Aufgaben und Lösungen
4.2 Multiplikation und Division
4.3 Lösungen
4.4 Wir wurzeln
4.4.1 √i und √8
4.4.2 z³ = i
4.4.3 z³ = 8
5. Die komplexe Exponentialfunktion
5.1. Die e-Funktion im Reellen
5.2 Exponentielles Wachstum
5.3 Das i im Exponenten macht den Kreis
5.4 Irrational und Imaginär: zusammen wird es natürlich
5.5. Formelön für Sinus und Cosinus
6. Vom Komplexen ins Chaos
6.1 Von Räubern und beute
6.2 Die logistische Gleichung
6.3 Material für ein Feigenbaumdiagramm
6.4 Das Feigenbaumdiagramm
6.5 Das Chaos im Feigenbaumdiagramm
6.6 Was ist Chaos?
7. Fraktale
7.1 Juliamengen
7.2 Apfelmännchen
7.3 Apfelmännchen und Feigenbaumdiagramm
7.4 Video
8. Hyperkomplexe Zahlen
Einschub: Aus Imaginär wird reell
9. Komplexe Funktionen
10. Wenn Strom komplex wird, wird alles leichter...
10.1 Der Kondensator
10.2 Die Spule
Zugabe: Experimente
10.3 Drehende Zeiger
10.4 Komplexe Widerstände
10.5. Vertiefungen
10.6 Wirk, Blind und Schein
10.7 Beispiel: Berechnung einer Brückenschaltung
Inhaltsverzeichnis
Zusatzseiten:
I. Überblick über Zahlsysteme
II. Rechenregel
III. Körperaxiome
IV. Ordnungsrelationen
V. Sinus und Cosinus
VI. Bogenmaß statt Winkel
VII. Lineare Funktionen
Donnerstag, 21. Mai 2020
Teil 10: Wenn Strom komplex wird, wird alles leichter...VII: Beispiel Berechnung einer Brückenschaltung
Zum Abschluss möchte ich einmal zeigen, wie man mit Hilfe der komplexen Widerstände in einem Rechengang Ströme und Phasen in einer Schaltung berechnen kann.
Die Rechnungen werden mit Texten eingeführt, sind als Bilder zu sehen und werden in Videos erläutert (sollten die falschen Videos auftauchen, bitte Browser beenden, bereinigen und neu starten...).
Zuerst stelle ich die Schaltung vor:
Es ist eine Brückenschaltung, d.h. längs der Seiten eines Quadrates sind Widerstände angeordnet und quer über die Diagonale (die Brücke) hinweg ebenfalls. Da so der Eindruck eines "H" entsteht, nennt man die Schaltung auch H-Schaltung.
Solche Schaltungen kommen mit ohmschen Widerständen häufig vor. Dabei ist ein Widerstand auf einer Quadratseite variabel. Ihn kann man so verstellen, dass in der Brücke kein Strom fließt.
Damit kann man z.B. sehr präzise Widerstände messen.
Wir wollen eine Brückenschaltung verwenden, die mit Wechselstrom arbeitet und dabei erreichen, dass der Strom über die Brücke von der Frequenz unabhängig ist. Das ist nur für einen bestimmten Brückenwiderstand möglich.
Hier die Schaltung und Video 1:
In der Elektrotechnik benutzt man Knoten- und Maschenregeln.
Ein Knoten ist eine Stelle, an der mehrere Leiter zusammentreffen, verknotet sind. Im Knoten darf kein Strom fließen, also muss die Summe aller hineinfließenden Ströme so groß sein wie die Summe aller herausfließenden Ströme.
Versieht man alle Ströme je nach Richtung mit einem Vorzeichen, so muss die Summe aller Ströme im Knoten 0 sein.
Damit fangen wir an:
Eine Masche ist ein in sich geschlossener Teilstromkreis. Die Summe aller Spannungen in einem Stromkreis muss immer 0 ergeben, das gilt auch in einer Masche. Durchlaufen wir dabei das Innere des Generators, müssen wir diese Spannung mit einem anderen Vorzeichen versehen.
Nun stellen wir die entsprechenden Gleichungen zusammen:
Jetzt haben wir alle Gleichungen zusammen. Die Phaseninformation für die Ströme setzen wir einfach in die komplexen Widerstände (*(-i)für Kondensator, *(+i) für Spule, *1 für ohmschen Widerstand).
Dann setzen wir für den ohmschen Widerstand den vorgegebenen Wert ein, für den die Unabhängigkeit von der Frequenz eintreten soll und rechnen die Stromstärke durch diesen Widerstand aus.
Und wir haben es geschafft...Die Formel für die komplexe Stromstärke enthält einen Real- und einen Imaginärteil. Damit kann man den messbaren Betrag der Stromstärke und die Phasenverschiebung zur angelegten Spannung ausrechnen.
Wie gewünwscht, hängt die Stromstärke nicht von der Frequenz ab, nur von C und L und der angelegten Spannung.
Es ergibt sich:
Io = √(C/L) * Uo, d.h. Uo = √(L/C) * Io...wer hätte das gedacht...
Fertig!
Mit dem nächsten Post schließen wir dann den Blog ab.
Die Rechnungen werden mit Texten eingeführt, sind als Bilder zu sehen und werden in Videos erläutert (sollten die falschen Videos auftauchen, bitte Browser beenden, bereinigen und neu starten...).
Zuerst stelle ich die Schaltung vor:
Es ist eine Brückenschaltung, d.h. längs der Seiten eines Quadrates sind Widerstände angeordnet und quer über die Diagonale (die Brücke) hinweg ebenfalls. Da so der Eindruck eines "H" entsteht, nennt man die Schaltung auch H-Schaltung.
Solche Schaltungen kommen mit ohmschen Widerständen häufig vor. Dabei ist ein Widerstand auf einer Quadratseite variabel. Ihn kann man so verstellen, dass in der Brücke kein Strom fließt.
Damit kann man z.B. sehr präzise Widerstände messen.
Wir wollen eine Brückenschaltung verwenden, die mit Wechselstrom arbeitet und dabei erreichen, dass der Strom über die Brücke von der Frequenz unabhängig ist. Das ist nur für einen bestimmten Brückenwiderstand möglich.
Hier die Schaltung und Video 1:
In der Elektrotechnik benutzt man Knoten- und Maschenregeln.
Ein Knoten ist eine Stelle, an der mehrere Leiter zusammentreffen, verknotet sind. Im Knoten darf kein Strom fließen, also muss die Summe aller hineinfließenden Ströme so groß sein wie die Summe aller herausfließenden Ströme.
Versieht man alle Ströme je nach Richtung mit einem Vorzeichen, so muss die Summe aller Ströme im Knoten 0 sein.
Damit fangen wir an:
 |
| Anwendung Maschen- und Knotenregel |
Eine Masche ist ein in sich geschlossener Teilstromkreis. Die Summe aller Spannungen in einem Stromkreis muss immer 0 ergeben, das gilt auch in einer Masche. Durchlaufen wir dabei das Innere des Generators, müssen wir diese Spannung mit einem anderen Vorzeichen versehen.
Nun stellen wir die entsprechenden Gleichungen zusammen:
Jetzt haben wir alle Gleichungen zusammen. Die Phaseninformation für die Ströme setzen wir einfach in die komplexen Widerstände (*(-i)für Kondensator, *(+i) für Spule, *1 für ohmschen Widerstand).
Dann setzen wir für den ohmschen Widerstand den vorgegebenen Wert ein, für den die Unabhängigkeit von der Frequenz eintreten soll und rechnen die Stromstärke durch diesen Widerstand aus.
Und wir haben es geschafft...Die Formel für die komplexe Stromstärke enthält einen Real- und einen Imaginärteil. Damit kann man den messbaren Betrag der Stromstärke und die Phasenverschiebung zur angelegten Spannung ausrechnen.
Wie gewünwscht, hängt die Stromstärke nicht von der Frequenz ab, nur von C und L und der angelegten Spannung.
Es ergibt sich:
Io = √(C/L) * Uo, d.h. Uo = √(L/C) * Io...wer hätte das gedacht...
Fertig!
Mit dem nächsten Post schließen wir dann den Blog ab.
Montag, 18. Mai 2020
Teil 10: Wenn Strom komplex wird, wird alles leichter...VI: Wirk, Blind und Schein....
Mit R bezeichnet man den reelllen Anteil, man nennt ihn Wirkwiderstand.
Formel:
R = Re(Z) = Z * cos φ
Dann gibt es nur den Imaginärteil des komplexen Widerstandes Z, es ist der Blindwiderstand X.
X = Im(Z) = Z * sin φ
Spannung und Stromstärke sind am Blindwiderstand um 90° phasenverschoben. Die Spannung kann am Strom keine Arbeit verrichten.
So etwas ähnliches kennen wir von der Kraft:
Wirkt die Kraft senkrecht zum Weg, so verrichtet sie ebenfalls keine Arbeit.
Die elektrische Energie fließt in den Blindwiderstand hinein, aber auch wieder heraus. Sie pendelt sozusagen zwischen Erzeuger und Verbraucher hin- und her.
Blindwiderstand X und Wirkwiderstand R müssen quadratisch zum Scheinwiderstand Z addiert werden:
Z² = X² + R²
In vielen elektrischen Geräten sind Spulen, sie erzeugen Blindwiderstände. Hat eine Firma viele solcher Geräte im Einsatz, muss sie die Phasenverschiebungen durch Kondensatorblöcke kompensieren.
Entsprechende Überlegungen gibt es auch für die Leistungen von Wechselstrom:
 |
| wordpress |
Und wer das nicht versteht, sollte sich mit einem kühlen Bier (alkoholfrei!) zurückziehen:
 |
| energiezentrum berlin |
Im nächsten Post zeige nich, wie man sich auch viele umständliche Rechnerei erspart...da machen wir mal eine Netzwerkrechnung mit komplexen Widerständen.
Teil 10: Wenn Strom komplex wird, wird alles leichter...V: Vertiefungen
In meinem Blog über Elektrotechnik sind einige Kapitel, die unseren Blog hier ergänzen. Sie sind aber zum weiteren Verständnis nicht wichtig.
Addition von Impedanzen: Problemdarstellung
Addition von Impedanzen: Einführung von Zeigerdiagrammen
Übungsaufgaben und Lösungen
Blindleistung
Addition von Impedanzen: Problemdarstellung
Addition von Impedanzen: Einführung von Zeigerdiagrammen
Übungsaufgaben und Lösungen
Blindleistung
Sonntag, 17. Mai 2020
Teil 10: Wenn Strom komplex wird, wird alles leichter...IV: Komplexe Widerstände
Rechnen wir erst einmal die Gesamtspannung aus:
Da die Zeiger die Maximalwerte angeben und diese bei gleicher Stromstärke I proportional zum jeweiligen Widerstand sind, kann man auch Widerstandszeiger einführen.
Nun, Spannungen als gerichtete Größen, ja, das kann man sich vorstellen...
Widerstände? Aber wenn wir die Zeichnung als Darstellung komplexer Zahlen auffassen, an die senkrechte Achse die Imaginäranteile antragen und an die waagerechte Achse die Realanteile, dann erhält jetzt jeder Widerstand einen komplexen Wert. Der Pfeil markiert also keine Richtung mehr, sondern ist eine Darstellung der komplexen Werte der Widerstände.
Diese werden üblicherweise nicht mit R sondern mit Z abgekürzt!
Und wir werden im nächsten Post sehen, welche physikalische Bedeutung sie haben.
Im übrigen: Hier wird deutlich, dass komplexe Zahlen keine Vektoren sind, wir können sie durch Pfeile markieren, so wie wir das eben bei Widerstände machen. Aber diese Pfeile weisen dann auf eine komplexe Zahl und nicht in eine Richtung!
Nicht alles, was man mit zwei Koordinaten angibt, ist ein Vektor!
(Für Fachleute: Vektoren sind zweikomponentige Tensoren, unterliegen also ganz bestimmten Eigenschaften beim Wechsel von Koordinatensystemen.)
Die komplexen Widerstände können wir nun ganz einfach hinschreiben:
Den ohmschen Widerstand haben wir als RΩ bezeichnet, der Pfeil liegt komplett auf der Realachse, also ist der komplexe Widerstand ZΩ = RΩ
Den Kondensatorwiderstand haben wir als 1/(ω *C) bezeichnet, er legt auf der imaginären Achse, also ist Zc= -i/( ω *C). -i, weil er ja nach unten zeigt.
Ganz entsprechend ist somit der komplexe induktive Widerstand Xl = i *ω * L.
Und der Gesamtwiderstand?
Einfach die drei komplexen Zahlen addieren:
Z = ZΩ + Zc+ Zl
Den Betrag dieser Zahl Z, also |Z| nennt man auch den Scheinwiderstand:
Der komplexe Gesamtwiderstand Z hat einen Real- und einen Imaginäranteil.
Was bedeutet dies physikalisch?
Darüber mehr im nächsten Post.
Samstag, 16. Mai 2020
Teil 10: Wenn Strom komplex wird, wird alles leichter...III: Drehende Zeiger
Bevor wir zu komplexen Widerständen kommen, möchte ich euch erst eine Methode vorstellen, mit der man die Kurven für I(t) und U(t) erzeugen kann:
Dazu müssen wir aus der Mathematik übernehmen, dass sich drehende Zeiger Sinus-Kurven erzeugen.
Man sagt in der Fachsprache: Die Projektion einer Kreisbewegung ist eine (harmonische) Schwingung.
In diesem Bild zu einer Federschwingung wird klar, was damit gemeint ist:
Wenn das Federpendel schwingt, kann man den Zeiger links im Bild sich immer so schnell drehen lassen (gegen den Uhrzeigersinn) , dass seine Spitze immer auf der Höhe der Pendelmasse ist. Trägt man dann den Abstand der Zeigerspitze von der Nulllage gegen die Zeit auf, so erhält man die typische Schwingungskurve ganz rechts.
Das haben wir auf den Infoseiten ja schon zusammengestellt:
Einheitskreis und Sinus
Die Zeigerlänge ist dabei die Amplitude der Schwingung, das wäre dann auch der Kreisradius.
Bei Wechselstrom interessieren uns zwei Schwingungen gleichzeitig, die des Stromes und die der Spannung...
Was machen wir? Wir nehmen zwei Zeiger...und drehen sie mit der gleichen Geschwindigkeit.
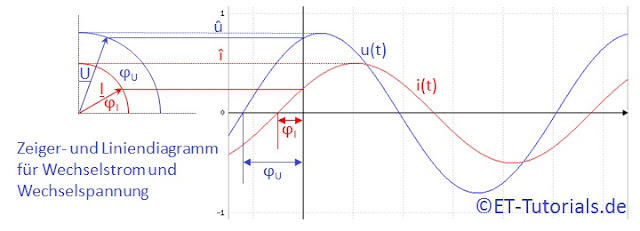
Das ist im nächsten Bild dargestellt:
Hier ist für den Winkel zwischen den Zeigern für Spannung und Stromstärke ein beliebiger Wert angenommen worden.
Das ist bei Spule und Kondensator einfacher (das steht in den letzten Posts):
Kondensator: Die Stromstärke eilt der Spannung immer um 90° voraus. Der Winkel zwischen den Zeigern für Spannung und Stromstärke am Kondensator muss also 90° sein.
Spule: Hier eilt die Spannung der Stromstärke um 90° voraus. Anders ausgedrückt: Die Stromstärke hinkt der Spannung um 90° hinterher. Die beiden Zeiger für Spannung und Stromstärke haben auch einen 90° - Winkel dazwischen, nur in der anderen Richtung als beim Kondensator gedreht.
Und wie ist es beim ohmschen Widerstand?
Da sind Spannung und Stromstärke gleichphasig, also liegen die Zeiger aufeinander!.
Am einfachsten verstehen wir die idee, wenn wir eine Riehenschaltung von Spule, Kondensator und ohmschen Widerstand betrachten.
Diese Schaltung spielt in der Wechselstromtechnik als Siebkette eine große Rolle. Das werden wir hier aber nicht verfolgen.
Durch alle drei Bauteile fließt der gleiche Strom, es gibt also einen einzigen Zeiger für I(t). Den legen wir auf die waagerechte Achse.
Der Zeiger für die Spannung am ohmschen Widerstand muss dann auczh, mit anderer Länge, dort liegen.
Da wir gegen den Uhrzeigersinn drehen wollen (ist so verabredetz), liegt der Zeiger für die Spannung am Kondensator dann um 90° verdreht nach unten. Nur so ist I vor U!
Und der Zeiger für die Spannung an der Spule eilt ja I(t) voraus, er liegt um 90° verdreht senkrecht nach oben.
Dazu müssen wir aus der Mathematik übernehmen, dass sich drehende Zeiger Sinus-Kurven erzeugen.
Man sagt in der Fachsprache: Die Projektion einer Kreisbewegung ist eine (harmonische) Schwingung.
In diesem Bild zu einer Federschwingung wird klar, was damit gemeint ist:
 |
| de scio de |
Das haben wir auf den Infoseiten ja schon zusammengestellt:
Einheitskreis und Sinus
Die Zeigerlänge ist dabei die Amplitude der Schwingung, das wäre dann auch der Kreisradius.
Bei Wechselstrom interessieren uns zwei Schwingungen gleichzeitig, die des Stromes und die der Spannung...
Was machen wir? Wir nehmen zwei Zeiger...und drehen sie mit der gleichen Geschwindigkeit.
Das ist im nächsten Bild dargestellt:
Hier ist für den Winkel zwischen den Zeigern für Spannung und Stromstärke ein beliebiger Wert angenommen worden.
Das ist bei Spule und Kondensator einfacher (das steht in den letzten Posts):
Kondensator: Die Stromstärke eilt der Spannung immer um 90° voraus. Der Winkel zwischen den Zeigern für Spannung und Stromstärke am Kondensator muss also 90° sein.
Spule: Hier eilt die Spannung der Stromstärke um 90° voraus. Anders ausgedrückt: Die Stromstärke hinkt der Spannung um 90° hinterher. Die beiden Zeiger für Spannung und Stromstärke haben auch einen 90° - Winkel dazwischen, nur in der anderen Richtung als beim Kondensator gedreht.
Und wie ist es beim ohmschen Widerstand?
Da sind Spannung und Stromstärke gleichphasig, also liegen die Zeiger aufeinander!.
Am einfachsten verstehen wir die idee, wenn wir eine Riehenschaltung von Spule, Kondensator und ohmschen Widerstand betrachten.
Diese Schaltung spielt in der Wechselstromtechnik als Siebkette eine große Rolle. Das werden wir hier aber nicht verfolgen.
 |
| schule-bw |
Der Zeiger für die Spannung am ohmschen Widerstand muss dann auczh, mit anderer Länge, dort liegen.
Da wir gegen den Uhrzeigersinn drehen wollen (ist so verabredetz), liegt der Zeiger für die Spannung am Kondensator dann um 90° verdreht nach unten. Nur so ist I vor U!
Und der Zeiger für die Spannung an der Spule eilt ja I(t) voraus, er liegt um 90° verdreht senkrecht nach oben.
Nun können wir aus den drei Einzelspannungen die Gesamtspannung ausrechnen. Das kann jeder ja mal probieren, mit Hilfe des ollen Griechen...
Und wer kann den Gesamtwiderstand der Schaltung angeben?
Damit machen wir im nächsten Post weiter.
Ich denke, einige ahnen schon, wie wir da mit komplexen Zahlen weitermachen können...Ich muss eigentlich nur noch Real und Im an die Achsen schreiben....
Intermezzo: Experimente
Ja, wir machen Mathematik...aber trotzdem können physikalische Experimente manchmal Dinge veranschaulichen.
Ich habe hier zwei Versuche gefilmt, bei denen man die Phasenverschiebung zwischen Strom und Spannung an Spule und Kondensator durch einen Trick am Oszilloskop sichtbar machen kann.
Zum Trick: Oszilloskope können nur Spannungen messen, keine Ströme. Deshalb habe ich einen kleinen Widerstand in Reihe geschaltet. Die Spannung, die an ihm abfällt (und die das Oszilloskop messen kann) ist proportional zum Strom, der durch den Widerstand fließt.
Ich habe hier zwei Versuche gefilmt, bei denen man die Phasenverschiebung zwischen Strom und Spannung an Spule und Kondensator durch einen Trick am Oszilloskop sichtbar machen kann.
Zum Trick: Oszilloskope können nur Spannungen messen, keine Ströme. Deshalb habe ich einen kleinen Widerstand in Reihe geschaltet. Die Spannung, die an ihm abfällt (und die das Oszilloskop messen kann) ist proportional zum Strom, der durch den Widerstand fließt.
Donnerstag, 14. Mai 2020
Teil 10: Wenn Strom komplex wird, wird alles leichter...II: Die Spule
Spulen bilden die Hauptbestandteile von Elektromagneten und Elektromotoren.
Ein Draht ist so aufgewickelt, dass die einzelnen Windungen spiralförmig eng aufeinanderliegen.
Da jeder elektrische Strom ein Magnetfeld hat, verdichten sich somit auch die Magnetfelder der einzelnen Drähte und heraus kommt ein Magnetfeld, das dem eines Stabmagneten ähnelt.
Bevor wir verstehen, was eine Spule mit Wechselstrom macht, müssen wir die Induktion kennen lernen:
Elektromagnetische Induktion,
oder:
Wie man Strom erzeugt oder dem Strom das Leben schwer macht...
Immer wenn sich ein Magnetfeld ändert, erzeugt es ein kreisförmiges elektrisches Feld, dass Ladungen kreisförmig in Bewegung setzt.
So stellen wir Strom her! Und so funktioniert der Induktionsherd.
Beim Generator drehen wir eine Spule in einem Magnetfeld. Da scheint sich zwar das Magnetfeld nicht zu ändern, aber die Menge der Feldlinien, die durch die Querschnittsfläche der Spule gehen, variiert durch die Drehung. Und deshalb entsteht in der Spule eine Wechselspannung.
Da jeder elektrische Strom ein eigenes Magnetfeld ist, behindert sich elektrischer Strom oft selbt:
Nehmen wir einen Wechselstrom, der durch eine Spule fließt. Der sich ständig ändernde und sich umpolende Strom erzeugt ein sich ständig änderndes Magnetfeld. Das wiederum muss ein kreisförmiges elektrisches Feld in der Spule erzeugen (man nennt das Selbstinduktion).
Damit der Energieerhaltungssatz gilt, muss dieses elektrische Feld den Strom, der es erzeugt, abschwächen. Sonst hätten wir ein Perpetuum Mobile...
Das gibt der Spule einen Widerstand gegen Wechselstrom.
Und somit haben wir die Ursache für den Wechselstromwiderstand gefunden:
Das sich ändernde Spulenmagnetfeld schwächt den eigenen Strom ab!
Da die Induktionsspannung größer ist, wenn die Änderung des Magnetfeldes schneller erfolgt, wächst der Wechselstromwiderstand Rl der Spule mit der Frequenz.
Es gilt:
Rl = ω * L
Hier bei ist L die Induktivität. Sie gibt an, wie stark die Spule auf Magnetfeldänderungen reagiert. Man kann L auch als die Trägheit des Magnetfeldes auffassen. Je größer L ist, desto träger reagiert das Magnetfeld und desto größer ist der Widerstand der Spule für Wechselstrom.
Erschwerend kommt hinzu, dass die Spule aus Draht besteht und somit dieser Draht einen ganz normalen ohmschen Widerstand besitzt. Den vernachlässigen wir hier.
Für uns ist aber etwas anderes sehr wichtig:
Wenn ich eine Spannung an eine Spule anlege, kommt der Stromfluss wegen der Selbstinduktion (Trägheit des Magnetfeldes: Es mag nicht aufgebaut werden, ist halt träge.....das gibt ihnen etwas menschliches...) nur verzögert zustande.
Eine mathematische Auswertung über Differenzialgleichungen ergibt:
Bei einer Spule hinkt die Stromstärkekurve I(t) der Spannungskurve U(t) um eine Viertel Periode, also um 90° hinterher.
Noch mal zur Erinnerung:
Bei einem Kondensator läuft I(t) um 90° vor der Spannungskurve und bei einer Spule um 90° nach der Spannungskurve.
Jetzt sind wir bereit, das alles durch komplexe Zahlen zusammenzufassen.
Ein Draht ist so aufgewickelt, dass die einzelnen Windungen spiralförmig eng aufeinanderliegen.
Da jeder elektrische Strom ein Magnetfeld hat, verdichten sich somit auch die Magnetfelder der einzelnen Drähte und heraus kommt ein Magnetfeld, das dem eines Stabmagneten ähnelt.
 | |
| JHMünster |
 |
| Experimentierspule, leybold |
Bevor wir verstehen, was eine Spule mit Wechselstrom macht, müssen wir die Induktion kennen lernen:
Elektromagnetische Induktion,
oder:
Wie man Strom erzeugt oder dem Strom das Leben schwer macht...
Immer wenn sich ein Magnetfeld ändert, erzeugt es ein kreisförmiges elektrisches Feld, dass Ladungen kreisförmig in Bewegung setzt.
So stellen wir Strom her! Und so funktioniert der Induktionsherd.
Beim Generator drehen wir eine Spule in einem Magnetfeld. Da scheint sich zwar das Magnetfeld nicht zu ändern, aber die Menge der Feldlinien, die durch die Querschnittsfläche der Spule gehen, variiert durch die Drehung. Und deshalb entsteht in der Spule eine Wechselspannung.
Da jeder elektrische Strom ein eigenes Magnetfeld ist, behindert sich elektrischer Strom oft selbt:
Nehmen wir einen Wechselstrom, der durch eine Spule fließt. Der sich ständig ändernde und sich umpolende Strom erzeugt ein sich ständig änderndes Magnetfeld. Das wiederum muss ein kreisförmiges elektrisches Feld in der Spule erzeugen (man nennt das Selbstinduktion).
Damit der Energieerhaltungssatz gilt, muss dieses elektrische Feld den Strom, der es erzeugt, abschwächen. Sonst hätten wir ein Perpetuum Mobile...
Das gibt der Spule einen Widerstand gegen Wechselstrom.
Und somit haben wir die Ursache für den Wechselstromwiderstand gefunden:
Das sich ändernde Spulenmagnetfeld schwächt den eigenen Strom ab!
Da die Induktionsspannung größer ist, wenn die Änderung des Magnetfeldes schneller erfolgt, wächst der Wechselstromwiderstand Rl der Spule mit der Frequenz.
Es gilt:
Rl = ω * L
Hier bei ist L die Induktivität. Sie gibt an, wie stark die Spule auf Magnetfeldänderungen reagiert. Man kann L auch als die Trägheit des Magnetfeldes auffassen. Je größer L ist, desto träger reagiert das Magnetfeld und desto größer ist der Widerstand der Spule für Wechselstrom.
Erschwerend kommt hinzu, dass die Spule aus Draht besteht und somit dieser Draht einen ganz normalen ohmschen Widerstand besitzt. Den vernachlässigen wir hier.
Für uns ist aber etwas anderes sehr wichtig:
Wenn ich eine Spannung an eine Spule anlege, kommt der Stromfluss wegen der Selbstinduktion (Trägheit des Magnetfeldes: Es mag nicht aufgebaut werden, ist halt träge.....das gibt ihnen etwas menschliches...) nur verzögert zustande.
Eine mathematische Auswertung über Differenzialgleichungen ergibt:
Bei einer Spule hinkt die Stromstärkekurve I(t) der Spannungskurve U(t) um eine Viertel Periode, also um 90° hinterher.
 |
| ETH Zürich |
Noch mal zur Erinnerung:
Bei einem Kondensator läuft I(t) um 90° vor der Spannungskurve und bei einer Spule um 90° nach der Spannungskurve.
Jetzt sind wir bereit, das alles durch komplexe Zahlen zusammenzufassen.
Wer noch etwas vertiefter arbeiten möchte, hier passende Links aus meinem anderen Blog:
Dienstag, 12. Mai 2020
Teil 10: Wenn Strom komplex wird, wird alles leichter...I: Der Kondensator
In der letzten Postrunde möchte ich noch eine Anwendung vorstellen, die zu großer Bedeutung gelangt ist:
Komplexe Widerstände
Wechselstrom:
Zuerst müsst ihr den Unterschied zwischen Gleichstrom und Wechselstrom kennen:
Batterien erzeugen Gleichstrom, eine fest orientierte Spannung lässt die Ladungen immer in die gleiche Richtung fließen.
Bei Wechselstrom ändert sich ständig die Stromrichtung, da die antreibende Spannung ihre Polung ständig ändert.
Der ohmsche Widerstand:
Wir alle kennen den normalen ohmschen Widerstand R = U/I, angegeben in Ohm Ω.
Ein Widerstand von 5 Ω bedeutet, dass man für einen Strom von 1 A einen Antrieb von 5 V braucht.
Je höher der Widerstand gegen den Strom ist, desto mehr Spannung benötigt man, um auf die gleiche Stromstärke zu kommen.
Irgendwie logisch...
Ohmsches Gesetz:
Die Formel U = R * I lernen Generationen von Jugendlichen. Dieses Gesetz sagt: Ist der Widerstand konstant, so sind U und I zueinander proportional.
Das gilt sogar für Wechselstrom:
Bei Wechselstrom wechselt etwa 60 mal in der Sekunde die Stromrichtung. Und immer ist der zu jedem Moment fließende Strom zur angelegten Spannung proportional.
Man sagt: U(t) und I(t) sind gleichphasig.
Kondensator im Stromkreis:
Ein Kondensator besteht aus zwei Metallplatten, die sich gegenüber stehen und die gegeneinander isoliert sind.
Beide Platten können durch eine angelegte Spannung U auf jeweils die Ladung Q (auf der einen Platte die positive Ladung Q+ und auf der anderen die negative Ladung Q-) aufgeladen werden.
Es gilt die Gleichung Q = C * U, dabei ist C die Kapazität des Kondensators. Sie gibt an, wieviel Ladung man pro Volt Antrieb auf die Platten bekommt.
Für einen Gleichstrom sperrt ein Kondensator den Stromfluß nachdem er aufgeladen ist.
Ein Wechselstrom spürt den Kondensator als Hindernis, er kann aber hin- und herfließen, so wie das für einen Wechselstrom halt üblich ist:
Der Strom lädt den Kondensator auf, dabei entsteht eine Spannung zwischen den geladenen Platten des Kondensators, die die Stromstärke reduziert. Wenn dann der Strom in die andere Richtung fließt ,kann der Kondensator sich weider entladen. Dieses ständige Auf- und Entladen erzeugt eine ständig wechselnde Spannung am Kondensator, die den Stromfluß behindert.
Der Kondensator hat also einen Wechselstromwiderstand.
Der ist für uns nicht wichtig, trotzdem gebe ich die Formel einmal an:
Rc = 1/(2π*f* C).
Ist die Frequenz f des Wechselstroms ganz hoch, so macht sich die Gegenspannung des Kondensators durch die Aufladung kaum bemerkbar, sein Widerstand für den Wechselstrom ist klein. Das gilt auch, wenn er eine große Kapazität hat, also leicht aufladbar ist.
Für uns ist aber etwas anderes wichtig:
Erst muss ein Strom auf die Kondensatorplatten fließen, damit dort eine Spannung entstehen kann. U(t) und I(t) sind nicht mehr gleichphasig.
Die Stromstärkekurve I(t) eilt der Spannugnskurve U(t) um ein Viertel der Periode des Wechselstroms voraus, also letztlich um 360°/4 = 90°.
Die Phasenverschiebung von U(t) und I(t) bei Wechselstrom ist 90°
Wie geht es weiter?
Im nächsten Post lernen wir die Spule im Wechselstromkreis kennen.
Dann nutzen wir die Phasenverschiebung von 90° aus, um das Verhalten des Wechselstromes mit Realteil und Imaginärteil von komplexen Zahlen zu beschreiben (Trick: Realteile und Imaginärteile komplexer Zahlen werden auch auf zueinander um 90° gedrehte Achsen dargestellt) und berechnen dann zum Schluß eine elektrische Schaltung mit komplexen Zahlen.
Dabei erhalten wir alle Informationen über die Schaltung schnell und relativ einfach!
Hinweis:
Ich habe noch einen zweiten Blog über Wechselstromtechnik.
Da sind viele der eben erwähnten Aspekte ausführlicher und mathematischer beschrieben. Ich gebe mal Links an, falls jemand etwas mehr und vertieft erfahren möchte, für uns hier im Blog ist das aber nicht wichtig:
Wechselstromwiderstände
Mehr mathematische Info zum Kondensator im Wechselstromkreis
Mehr Infos zum Begriff der Kapazität
Komplexe Widerstände
Wechselstrom:
Zuerst müsst ihr den Unterschied zwischen Gleichstrom und Wechselstrom kennen:
Batterien erzeugen Gleichstrom, eine fest orientierte Spannung lässt die Ladungen immer in die gleiche Richtung fließen.
Bei Wechselstrom ändert sich ständig die Stromrichtung, da die antreibende Spannung ihre Polung ständig ändert.
Der ohmsche Widerstand:
Wir alle kennen den normalen ohmschen Widerstand R = U/I, angegeben in Ohm Ω.
Ein Widerstand von 5 Ω bedeutet, dass man für einen Strom von 1 A einen Antrieb von 5 V braucht.
Je höher der Widerstand gegen den Strom ist, desto mehr Spannung benötigt man, um auf die gleiche Stromstärke zu kommen.
Irgendwie logisch...
Ohmsches Gesetz:
Die Formel U = R * I lernen Generationen von Jugendlichen. Dieses Gesetz sagt: Ist der Widerstand konstant, so sind U und I zueinander proportional.
Das gilt sogar für Wechselstrom:
Bei Wechselstrom wechselt etwa 60 mal in der Sekunde die Stromrichtung. Und immer ist der zu jedem Moment fließende Strom zur angelegten Spannung proportional.
Man sagt: U(t) und I(t) sind gleichphasig.
Kondensator im Stromkreis:
Ein Kondensator besteht aus zwei Metallplatten, die sich gegenüber stehen und die gegeneinander isoliert sind.
Beide Platten können durch eine angelegte Spannung U auf jeweils die Ladung Q (auf der einen Platte die positive Ladung Q+ und auf der anderen die negative Ladung Q-) aufgeladen werden.
Es gilt die Gleichung Q = C * U, dabei ist C die Kapazität des Kondensators. Sie gibt an, wieviel Ladung man pro Volt Antrieb auf die Platten bekommt.
Für einen Gleichstrom sperrt ein Kondensator den Stromfluß nachdem er aufgeladen ist.
Ein Wechselstrom spürt den Kondensator als Hindernis, er kann aber hin- und herfließen, so wie das für einen Wechselstrom halt üblich ist:
Der Strom lädt den Kondensator auf, dabei entsteht eine Spannung zwischen den geladenen Platten des Kondensators, die die Stromstärke reduziert. Wenn dann der Strom in die andere Richtung fließt ,kann der Kondensator sich weider entladen. Dieses ständige Auf- und Entladen erzeugt eine ständig wechselnde Spannung am Kondensator, die den Stromfluß behindert.
Der Kondensator hat also einen Wechselstromwiderstand.
Der ist für uns nicht wichtig, trotzdem gebe ich die Formel einmal an:
Rc = 1/(2π*f* C).
Ist die Frequenz f des Wechselstroms ganz hoch, so macht sich die Gegenspannung des Kondensators durch die Aufladung kaum bemerkbar, sein Widerstand für den Wechselstrom ist klein. Das gilt auch, wenn er eine große Kapazität hat, also leicht aufladbar ist.
Für uns ist aber etwas anderes wichtig:
Erst muss ein Strom auf die Kondensatorplatten fließen, damit dort eine Spannung entstehen kann. U(t) und I(t) sind nicht mehr gleichphasig.
Die Stromstärkekurve I(t) eilt der Spannugnskurve U(t) um ein Viertel der Periode des Wechselstroms voraus, also letztlich um 360°/4 = 90°.
Die Phasenverschiebung von U(t) und I(t) bei Wechselstrom ist 90°
Wie geht es weiter?
Im nächsten Post lernen wir die Spule im Wechselstromkreis kennen.
Dann nutzen wir die Phasenverschiebung von 90° aus, um das Verhalten des Wechselstromes mit Realteil und Imaginärteil von komplexen Zahlen zu beschreiben (Trick: Realteile und Imaginärteile komplexer Zahlen werden auch auf zueinander um 90° gedrehte Achsen dargestellt) und berechnen dann zum Schluß eine elektrische Schaltung mit komplexen Zahlen.
Dabei erhalten wir alle Informationen über die Schaltung schnell und relativ einfach!
Hinweis:
Ich habe noch einen zweiten Blog über Wechselstromtechnik.
Da sind viele der eben erwähnten Aspekte ausführlicher und mathematischer beschrieben. Ich gebe mal Links an, falls jemand etwas mehr und vertieft erfahren möchte, für uns hier im Blog ist das aber nicht wichtig:
Wechselstromwiderstände
Mehr mathematische Info zum Kondensator im Wechselstromkreis
Mehr Infos zum Begriff der Kapazität
Montag, 11. Mai 2020
Teil 9: Komplexe Funktionen
In diesem Abschnitt möchte ich einige anschauliche und unerwartete Eigenschaften zu komplexen Funktionen (ohne Beweis und nähere Begründung) angeben.
Wer sich damit beschäftigen will, muss sich in der höheren Mathematik mit Funktionentheorie auseinandersetzen.
Eine komplexe Funktion f(z) bildet einen Punkt z = x+iy = (x,y) auf einen anderen Punkt f(z) = (u,v) der komplexen Ebene ab:
Auch f(z) hat dann einen Realteil u und einen Imaginärteil v:
f(z) = u(x,y) + i* v(x,y)
Beispiel sei die komplexe Exponentialfunktion:
f(z) = exp(z) = exp(x)* (cos y + i*sin y)
Hier ist u(x,y) = exp(x) * cos y und v(x,y) = exp(x)*sin y
Auf diesmemBild drückt die Höhe den Realteil der komplexen Exponentialfunktion aus und die Farbe kodiert den Imaginärteil (aus Ahrends u.a. Mathematik, SpektrumVerlag).
Hier sehen wir f(z) = sin z, auch wieder mit der Höhe für den Realteil und die Farbe für den Imaginärteil. Man erkennt die periodisch liegenden Nullstellen auf der reellen Achse.
Sind komplexe Funktionen innerhalb eines Gebietes der komplexen Ebene ableitbar (Steigungen bestimmbar), so nennt man sie holomorph oder analytisch.
Dann kann man sie ganz normal ableiten:
f(z) = 3z² + 4z + 1 hat als Ableitung f´(z) = 6z +4
f(z) = sin z hat als Ableitung f´(z) = cos z
und exp´(z) = exp(z), wie im Reellen.
Auch das Integrieren (Aufsummieren) funktioniert vergleichbar. Es treten aber erstaunliche Vereinfachungen auf:
- Integrale sind vom Integrationsweg unabhängig.
- Kreisintegrale ergeben immer 0, wenn innerhalb des Kreises die Funktion ableitbar ist, insbesondere keine Polstellen auftreten. Das ist das berühmte Theorem von Cauchy.
- Liegen Polstellen innerhalb des Integrationskreises, so ergeben sich auch einfache Formeln (Residuensatz), wie bei f(z) = 1/z und einem Integrationsweg um z=0 herum:
Integriert man z.B. um z = 17i herum, ohne dass die Kurve den Ursprung einschließt, so ist das Integral wieder 0.
Fachleute kennen diese Eigenschaften von elektrischen Feldern her:
Nimmt man die klassische Feldstärke als Imaginärteil und das Potenzial als Realteil, so erhält man das komplexe elektrische Feld.
Im elektrischen Feld sind Kreisintegrale 0 (Die Summe aller Spannungen im Stromkreis ist 0, elektrische Felder sind wirbelfrei).
Ganz allgemein kann man sagen:
Ist die Funktion f(z) = u(x,y) + i* v(x,y) in einem Bereich differenzierbar, so stehen die Linien u(x,y) für festes y und v(x,y) für festes x senkrecht aufeinander, so wie Feldlinien und Äquipotenziallinien.
Mit komplexen Funktionen kann man auch Ähnlichkeitsabbildungen beschreiben. Insbesondere dreht f(z) = z* exp(iy) alles um den Winkel y und bildet f(z) = 1/z das Innere des Einheitskreises auf das Äußere ab (und umgekehrt).
Vergleiche: Die Funktion f(x) = 1/x bildet das Innere des Intervalls [-1,1] auf das Äußere auf dem Zahlenstrahl ab und umgekehrt.
Und auch sonst erleichtern komplexe, ableitbare Funktionen das Leben:
Die Werte auf einer geschlossenen Linie bestimmen alle Werte und Steigungen der Punkte innerhalb der Linie.
Stimmen zwei solcher Funktionen längs einer Linie überein, so sind sie in d r ganzen Ebene identisch.
Abschließend sei noch der Fundamentalsatz der Algebra angegeben (den wir indirekt schon beim Wurzeln kennengelernt haben):
Setzt man ein komplexes Polynom vom Grad n gleich 0, so erhält man eine Gleichung, die genau n Lösungen hat.
Wir haben davon genutzt:
Eine dritte Wurzel hat 3, eine vierte Wurzel 4 ...Werte. usw. Vielleicht erinnert man sich an die gleichseitigen Dreiecke, an deren Ecken die Wurzeln stehen.
In dne nächsten Posts kommen wir zum letzten Kapitel:
Komplexe Zahlen erleichtern Elektrotechnikern das Leben...
Wer sich damit beschäftigen will, muss sich in der höheren Mathematik mit Funktionentheorie auseinandersetzen.
Eine komplexe Funktion f(z) bildet einen Punkt z = x+iy = (x,y) auf einen anderen Punkt f(z) = (u,v) der komplexen Ebene ab:
Auch f(z) hat dann einen Realteil u und einen Imaginärteil v:
f(z) = u(x,y) + i* v(x,y)
Beispiel sei die komplexe Exponentialfunktion:
f(z) = exp(z) = exp(x)* (cos y + i*sin y)
Hier ist u(x,y) = exp(x) * cos y und v(x,y) = exp(x)*sin y
Auf diesmemBild drückt die Höhe den Realteil der komplexen Exponentialfunktion aus und die Farbe kodiert den Imaginärteil (aus Ahrends u.a. Mathematik, SpektrumVerlag).
 |
| (aus Ahrends u.a. Mathematik, SpektrumVerlag) |
Hier sehen wir f(z) = sin z, auch wieder mit der Höhe für den Realteil und die Farbe für den Imaginärteil. Man erkennt die periodisch liegenden Nullstellen auf der reellen Achse.
Sind komplexe Funktionen innerhalb eines Gebietes der komplexen Ebene ableitbar (Steigungen bestimmbar), so nennt man sie holomorph oder analytisch.
Dann kann man sie ganz normal ableiten:
f(z) = 3z² + 4z + 1 hat als Ableitung f´(z) = 6z +4
f(z) = sin z hat als Ableitung f´(z) = cos z
und exp´(z) = exp(z), wie im Reellen.
Auch das Integrieren (Aufsummieren) funktioniert vergleichbar. Es treten aber erstaunliche Vereinfachungen auf:
- Integrale sind vom Integrationsweg unabhängig.
- Kreisintegrale ergeben immer 0, wenn innerhalb des Kreises die Funktion ableitbar ist, insbesondere keine Polstellen auftreten. Das ist das berühmte Theorem von Cauchy.
- Liegen Polstellen innerhalb des Integrationskreises, so ergeben sich auch einfache Formeln (Residuensatz), wie bei f(z) = 1/z und einem Integrationsweg um z=0 herum:
Integriert man z.B. um z = 17i herum, ohne dass die Kurve den Ursprung einschließt, so ist das Integral wieder 0.
Fachleute kennen diese Eigenschaften von elektrischen Feldern her:
Nimmt man die klassische Feldstärke als Imaginärteil und das Potenzial als Realteil, so erhält man das komplexe elektrische Feld.
Im elektrischen Feld sind Kreisintegrale 0 (Die Summe aller Spannungen im Stromkreis ist 0, elektrische Felder sind wirbelfrei).
Ganz allgemein kann man sagen:
Ist die Funktion f(z) = u(x,y) + i* v(x,y) in einem Bereich differenzierbar, so stehen die Linien u(x,y) für festes y und v(x,y) für festes x senkrecht aufeinander, so wie Feldlinien und Äquipotenziallinien.
Mit komplexen Funktionen kann man auch Ähnlichkeitsabbildungen beschreiben. Insbesondere dreht f(z) = z* exp(iy) alles um den Winkel y und bildet f(z) = 1/z das Innere des Einheitskreises auf das Äußere ab (und umgekehrt).
Vergleiche: Die Funktion f(x) = 1/x bildet das Innere des Intervalls [-1,1] auf das Äußere auf dem Zahlenstrahl ab und umgekehrt.
Und auch sonst erleichtern komplexe, ableitbare Funktionen das Leben:
Die Werte auf einer geschlossenen Linie bestimmen alle Werte und Steigungen der Punkte innerhalb der Linie.
Stimmen zwei solcher Funktionen längs einer Linie überein, so sind sie in d r ganzen Ebene identisch.
Abschließend sei noch der Fundamentalsatz der Algebra angegeben (den wir indirekt schon beim Wurzeln kennengelernt haben):
Setzt man ein komplexes Polynom vom Grad n gleich 0, so erhält man eine Gleichung, die genau n Lösungen hat.
Wir haben davon genutzt:
Eine dritte Wurzel hat 3, eine vierte Wurzel 4 ...Werte. usw. Vielleicht erinnert man sich an die gleichseitigen Dreiecke, an deren Ecken die Wurzeln stehen.
In dne nächsten Posts kommen wir zum letzten Kapitel:
Komplexe Zahlen erleichtern Elektrotechnikern das Leben...
Intermezzo: Aus Imaginär wird Reell
Im Post vom 21.4.
Irrational und imaginär zusammen wird natürlich
haben wir schon gesehen, dass exp(iπ) = -1 ist und exp(2πi) = 1 ergibt.
Um das zu zeigen haben wir mit der Eulerschen Formel gearbeitet:
exp(iy) = cos y + i*sin y.
Letztlich ist das die Definition der komplexen Exponentialfunktion.
Wer sich das nochmal im Blog ansehen will:
Begründung der Eulerschen Formel
Nun wollen wir eins drauf setzen und wollen i hoch i berechnen...also etwas Imaginäres mit etwas Imaginären potenzieren...heraus kommt eine rein irrationale Zahl, also eine reelle Zahl...provozierend: knapp 21%...
iⁱ = 0,207879... ~21%
Um das zu beweisen, müssen wir erst i darstellen:
i liegt auf der imaginären Achse bei i, also ist in der Eulerschen Formel der Winkel y = 90° oder π/2.
Damit können wir über die Eulersche Formel i als Exponentialfunktion ausdrücken und somit auch mit i potenzieren..
Ich habe das mal aufgeschrieben:
Wer will, kann sich auch das folgende Video ansehen.
Hier wird das über den Logarithmus hergeleitet.
Ist etwas umständlicher, aber man lernt einen anderen Weg kennen und vorher wiederholt er Vieles, was wir gemacht haben. Er benutzt aber x statt y. Wir haben in usnerem Blog x für einen Realanteil und y für einen Imaginäranteil reserviert.
Im nächsten Post will ich kurz einige interessante Anmerkungen machen zum Ausführen von Kreisintegralen.
Was passiert, wenn man komplexe Funktionen im Kreis aufsummiert.... Wer sich mit Integralen nicht auskennt, kann das auch überspringen, es ist später nicht wichtig.
Zum Abschluss des Workshops möchte ich dann einmal die Anwendung komplexer Zahlen in der Elektrotechnik zeigen, also bei der Berechnung von Widerständen und Schaltungen.
Irrational und imaginär zusammen wird natürlich
haben wir schon gesehen, dass exp(iπ) = -1 ist und exp(2πi) = 1 ergibt.
Um das zu zeigen haben wir mit der Eulerschen Formel gearbeitet:
exp(iy) = cos y + i*sin y.
Letztlich ist das die Definition der komplexen Exponentialfunktion.
Wer sich das nochmal im Blog ansehen will:
Begründung der Eulerschen Formel
Nun wollen wir eins drauf setzen und wollen i hoch i berechnen...also etwas Imaginäres mit etwas Imaginären potenzieren...heraus kommt eine rein irrationale Zahl, also eine reelle Zahl...provozierend: knapp 21%...
iⁱ = 0,207879... ~21%
Um das zu beweisen, müssen wir erst i darstellen:
i liegt auf der imaginären Achse bei i, also ist in der Eulerschen Formel der Winkel y = 90° oder π/2.
Damit können wir über die Eulersche Formel i als Exponentialfunktion ausdrücken und somit auch mit i potenzieren..
Ich habe das mal aufgeschrieben:
Wer will, kann sich auch das folgende Video ansehen.
Hier wird das über den Logarithmus hergeleitet.
Ist etwas umständlicher, aber man lernt einen anderen Weg kennen und vorher wiederholt er Vieles, was wir gemacht haben. Er benutzt aber x statt y. Wir haben in usnerem Blog x für einen Realanteil und y für einen Imaginäranteil reserviert.
Im nächsten Post will ich kurz einige interessante Anmerkungen machen zum Ausführen von Kreisintegralen.
Was passiert, wenn man komplexe Funktionen im Kreis aufsummiert.... Wer sich mit Integralen nicht auskennt, kann das auch überspringen, es ist später nicht wichtig.
Zum Abschluss des Workshops möchte ich dann einmal die Anwendung komplexer Zahlen in der Elektrotechnik zeigen, also bei der Berechnung von Widerständen und Schaltungen.
Samstag, 9. Mai 2020
Teil 8: Hyperkomplexe Zahlen
Bevor wir uns weiteren Anwendungen und Beispielen zuwenden, ein ganz kurzer Blick auf noch komplexere Zahlsysteme:
Quaternionen:
Zahlen der Form a +b* i + c*j + d*k wobei i = j = k = √(-1) und i*j*k = -1 sein muss.
Es sind also vierdimensionale Punkte (a,b,c,d)
Anwendung: Mit der Multiplikation von Quaternionen kann man Drehungen im Raum gut beschreiben. Dabei ist die erste Komponente eine skalere Größe und die anderen drei Komponenten liefern Vektoren.
Nachteil: Produkte sind nicht immer kommutativ, d.h. q*p muss nicht p*q sein.
Wer etwas mehr darüber lernen will, auch wie man Quaternionen addiert, sollte sich dieses (englischsprachige) Video ansehen:
Oktonionen:
Hier gibt es eine reelle und sieben imaginäre Einheiten.
Nachteil: Das Assoziativgesetz für die Multiplikation dieser achtdimensionalen Zahlen gilt nicht mehr.
Sedenionen:
Eine reelle und 15 imaginäre Einheiten liefern Zahlen mit 16 Dimensionen.
Nachteil: Es gibt Nullteiler, d.h. zu einer Zahl A gibt es eine Zahl B, die nicht 0 ist, aber trotzdem A*B = 0 liefert.
In der Schule nutzen wir aus, dass in den üblichen Zahlenmengen keine Nullteiler existieren.
Deshalb können wir sagen:
Ein Produkt a*b ist 0, wenn einer der beiden Faktoren a oder b gleich 0 ist.
Das hilft uns, viele Gleichungen einfach zu lösen: (x -5) * (3x+7) = 0 ergibt x = 5 oder x = -7/3
Würden wir in 16 Dimensionen rechnen, wäre das nicht so einfach...
Quaternionen:
Zahlen der Form a +b* i + c*j + d*k wobei i = j = k = √(-1) und i*j*k = -1 sein muss.
Es sind also vierdimensionale Punkte (a,b,c,d)
Anwendung: Mit der Multiplikation von Quaternionen kann man Drehungen im Raum gut beschreiben. Dabei ist die erste Komponente eine skalere Größe und die anderen drei Komponenten liefern Vektoren.
Nachteil: Produkte sind nicht immer kommutativ, d.h. q*p muss nicht p*q sein.
Wer etwas mehr darüber lernen will, auch wie man Quaternionen addiert, sollte sich dieses (englischsprachige) Video ansehen:
Oktonionen:
Hier gibt es eine reelle und sieben imaginäre Einheiten.
Nachteil: Das Assoziativgesetz für die Multiplikation dieser achtdimensionalen Zahlen gilt nicht mehr.
Sedenionen:
Eine reelle und 15 imaginäre Einheiten liefern Zahlen mit 16 Dimensionen.
Nachteil: Es gibt Nullteiler, d.h. zu einer Zahl A gibt es eine Zahl B, die nicht 0 ist, aber trotzdem A*B = 0 liefert.
In der Schule nutzen wir aus, dass in den üblichen Zahlenmengen keine Nullteiler existieren.
Deshalb können wir sagen:
Ein Produkt a*b ist 0, wenn einer der beiden Faktoren a oder b gleich 0 ist.
Das hilft uns, viele Gleichungen einfach zu lösen: (x -5) * (3x+7) = 0 ergibt x = 5 oder x = -7/3
Würden wir in 16 Dimensionen rechnen, wäre das nicht so einfach...
 |
| wikipedia |
Freitag, 8. Mai 2020
Intermezzo: Videoabend
Aus der Reihe Physics Videos by Eugene Khutoryansky gibt es auch ein schönes Video über komplexe Zahlen.
Die Reihe enthält viele, mit abstrakten aber sehr anschaulichen Darstellungen versehene Infos über weite Bereiche der Physik und Technik, mit dem musikalischen Hintergrund manchmal sehr gewöhnungsbedürftig, aber inhaltlich sehr sehr oft spitze.
Donnerstag, 7. Mai 2020
Teil 7: Das Apfelmännchen und Juliamengen
Betrachten wir noch einmal unsere Folge von komplexen Zahlen z(n+1) = z(n)² + c.
Die Konstante c hat zweierlei Funktionen:
1) c legt eine Juliamenge Jc fest, in dieser Juliamenge sind alle Startwerte, die zu einer konvergierenden Folge führen.
2) c ist ein Punkt in der Mandelbrotmenge, für dieses c bleibt die Folge bei einem Startwert von 0 beschränkt.
Hier ist der Zusammenhang zwischen c und der Lage in der Mandelbrotmenge dargestellt (Punkte 1 und i auf den Achsen markiert):
Das riecht nach einem Zusammenhang zwischen Mandelbrotmenge und Juliamenge:
- Wenn der Punkt c in der Mandelbrotmenge liegt, dann ist die zugehörende Juliamenge Jc in sich zusammenhängend. Das heißt vereinfacht: Jeder Punkt der Menge kann von jedem anderen Punkt über Wege erreicht werden, die komplett in der Menge liegen.
- Wenn c nicht in der Mandelbrotmenge liegt, dann ist die zugehörige Juliamenge "zerfleddert".
- Wenn man innerhalb der Mandelbrotmenge auf einen Punkt c zu zoomt, taucht am Ende irgendwann die Juliamenge Jc auf.
Im Bild oben sehen wir die Juliamengen zu einzelnen Mandelbrotpunkten.
Ein absoluter Hammer ist das Simulationsprogramm dazu, das man sich hier herunterladen kann:
Julia und Mandelbrot
Während die Punkte c durch die Mandelbrotmenge wandern, sieht man die zugehörigen Juliamengen.
Ein weiteres Simulationsprogramm kann im virtuellen Physiklabor von Prof. Matzdorf heruntergeladen werden:
Mandelbrot in Kassel
Begründungen für diese Zusammenhänge können wir hier nicht geben, stattdessen verlinke ich mal einige Videos, mit denen man abschließend eine Reise in die Unendlichkeit der Mandelbrotstrukturen machen kann:
750 Millionen Schritte:
Und wer selbst herumspielen möchte:
Zoom in die Mandelbrotmenge
Und immer wieder taucht ein neues Apfelbrotmännchen in der Tiefe auf...
Und nicht vergessen: Wir quadrieren nur komplexe Zahlen und zählen eine feste Zahl dazu...und erzeugende eine unfassbare Welt aus komplexen und ästhetischen Objekten:
Die fraktale Welt von Mandelbrot und Julia.
Die Konstante c hat zweierlei Funktionen:
1) c legt eine Juliamenge Jc fest, in dieser Juliamenge sind alle Startwerte, die zu einer konvergierenden Folge führen.
2) c ist ein Punkt in der Mandelbrotmenge, für dieses c bleibt die Folge bei einem Startwert von 0 beschränkt.
Hier ist der Zusammenhang zwischen c und der Lage in der Mandelbrotmenge dargestellt (Punkte 1 und i auf den Achsen markiert):
Das riecht nach einem Zusammenhang zwischen Mandelbrotmenge und Juliamenge:
- Wenn der Punkt c in der Mandelbrotmenge liegt, dann ist die zugehörende Juliamenge Jc in sich zusammenhängend. Das heißt vereinfacht: Jeder Punkt der Menge kann von jedem anderen Punkt über Wege erreicht werden, die komplett in der Menge liegen.
- Wenn c nicht in der Mandelbrotmenge liegt, dann ist die zugehörige Juliamenge "zerfleddert".
- Wenn man innerhalb der Mandelbrotmenge auf einen Punkt c zu zoomt, taucht am Ende irgendwann die Juliamenge Jc auf.
Im Bild oben sehen wir die Juliamengen zu einzelnen Mandelbrotpunkten.
Ein absoluter Hammer ist das Simulationsprogramm dazu, das man sich hier herunterladen kann:
Julia und Mandelbrot
Während die Punkte c durch die Mandelbrotmenge wandern, sieht man die zugehörigen Juliamengen.
Ein weiteres Simulationsprogramm kann im virtuellen Physiklabor von Prof. Matzdorf heruntergeladen werden:
Mandelbrot in Kassel
Begründungen für diese Zusammenhänge können wir hier nicht geben, stattdessen verlinke ich mal einige Videos, mit denen man abschließend eine Reise in die Unendlichkeit der Mandelbrotstrukturen machen kann:
750 Millionen Schritte:
Und wer selbst herumspielen möchte:
Zoom in die Mandelbrotmenge
Und immer wieder taucht ein neues Apfelbrotmännchen in der Tiefe auf...
Und nicht vergessen: Wir quadrieren nur komplexe Zahlen und zählen eine feste Zahl dazu...und erzeugende eine unfassbare Welt aus komplexen und ästhetischen Objekten:
Die fraktale Welt von Mandelbrot und Julia.
Mittwoch, 6. Mai 2020
Teil 7: Apfelmännchen und Feigenbaum
Wir haben ja schon gesehen, dass es bei der Mandelbrotmenge Punkte c gibt, die Folgen auf einen oder zwei oder mehr Endwerrte generieren.
Hier ist ein kleiner Überblick dazu:
Die Zahlen geben an, wieviele Endwerte es gibt.Vergrößert das Bild mal durch Anklicken.
Solche Bifurkationen haben wir schon beim Feigenbaum kennengelernt:
Alle Darstellungen sind von Georg Johann Lay.
Das Feigenbaumdiagramm ist umgekehrt angeordnet, damit man das besser zuordnen kann.
Hier ist ein kleiner Überblick dazu:
Die Zahlen geben an, wieviele Endwerte es gibt.Vergrößert das Bild mal durch Anklicken.
Solche Bifurkationen haben wir schon beim Feigenbaum kennengelernt:
Alle Darstellungen sind von Georg Johann Lay.
Das Feigenbaumdiagramm ist umgekehrt angeordnet, damit man das besser zuordnen kann.
Dienstag, 5. Mai 2020
Teil 7: Das Apfelmännchen II
und wie weit seid ihr??
wie, nicht weiter?
Ich hab das hier:
Im Inneren des Schwarzen liegen alle Zahlen für c, die Folgen mit einer Beschränkung unter 2 liefern. Die Farben und Tönungen markieren ab wieviel Rechenschritten klar ist, dass die Folge divergiert, also die Abstände über die 2 gehen.
Die folgenden Bilder (von Wolfgang Beyer mit Ultra Fractal 3 angefertigt) zeigen einige vergrößerte Ausschnitte, wir zoomen rein:
Überall lauern Kopien des Apfelbrotmännchens...eine wahrlich fraktale Struktur!
Und das sind nur komplexe Zahlen, die der Rechenanweisung folgen: Quadriere und addiere c dazu...
Und hier ein allgemein zugängliches Zoom-Video:
In den nächsten Posts werden wir mehr über die Mandelbrotmenge erfahren, auch den faszinierenden Zusammenhang zu den Juliamengen herstellen.
Dann werde ich einen Ausblick auf noch umfassendere Zahlbereiche geben (Quaterionen) und zum Abschluss gibt es noch einen kleinen Exkurs zur Anwendung komplexer Zahlen bei Wechselstrom.
So in einer knappen Woche ist der Kurs fertig.
wie, nicht weiter?
Ich hab das hier:
Im Inneren des Schwarzen liegen alle Zahlen für c, die Folgen mit einer Beschränkung unter 2 liefern. Die Farben und Tönungen markieren ab wieviel Rechenschritten klar ist, dass die Folge divergiert, also die Abstände über die 2 gehen.
Die folgenden Bilder (von Wolfgang Beyer mit Ultra Fractal 3 angefertigt) zeigen einige vergrößerte Ausschnitte, wir zoomen rein:
Überall lauern Kopien des Apfelbrotmännchens...eine wahrlich fraktale Struktur!
Und das sind nur komplexe Zahlen, die der Rechenanweisung folgen: Quadriere und addiere c dazu...
Und hier ein allgemein zugängliches Zoom-Video:
In den nächsten Posts werden wir mehr über die Mandelbrotmenge erfahren, auch den faszinierenden Zusammenhang zu den Juliamengen herstellen.
Dann werde ich einen Ausblick auf noch umfassendere Zahlbereiche geben (Quaterionen) und zum Abschluss gibt es noch einen kleinen Exkurs zur Anwendung komplexer Zahlen bei Wechselstrom.
So in einer knappen Woche ist der Kurs fertig.
Teil 7: Das Apfelmännchen I
Fachlich spricht man von der Mandelbrotmenge nach Benoit Mandelbrot, der sie 1980 näher untersucht hat.
Wir beschäftigen uns wieder mit unserer Gleichung z(n+1) = z(n)² + c mit komplexen Zahlen.
Zur Erinnerung: Eine Juliamenge Jc gehört zu einem bestimmten Wert von c und enthält die Startwerte, für die gerade noch eine Konvergenz der Folge von Zahlen z(n) vorliegt.
Jetzt nehmen wir einen festen Startwert, nämlich die reelle Zahl z(0) = 0. Wir arbeiten mit den Konstanten c, für die die Folge der Zahlen z(n) beschränkt bleibt, also z.B. |z(n)| < 2.
Ich hab mir das mal in ein Schema aufgeschrieben:
In einer zu c gehörenden Juliamenge werden also bestimmte Startwerte aufgetragen.
In der Mandelbrotmenge (sie gehört immer zum Startwert 0) werden bestimmte Konstanten der Folgen aufgetragen.
Über meinem Text stehen die Bedingungen zum Auftragen.
In den folgenden Rechnungen schreibe ich die ersten Folgenglieder der Folge z(n) hin:
Beispiel c = 0:
0+0 = 0,
0+0 = 0, usw.
c=0 liefert also eine beschränkte Folge, sie bleibt imemr auf dem Startwert hängen, der auf dem Urspung liegt.. Der Punkt c =0 gehört zur Mandelbrotmenge.
Beispiel c = -1:
0 - 1 = -1,
(-1)² + (-1) = 0
dann: -1, 0, -1, 0...
c= -1 liefert zwei Endwerte, die abwechselnd angenommen werden und die nicht weiter als 2 vom Urspung entfernt liegen. Der Punkt c = -1 gehört zur Mandelbrotmenge. Man sagt, er gehört zu zwei Grenzzyklen.
Hinweis: c = -1 ist eine komplexe Zahl mit dem Realteil -1 und dem Imaginärteil 0.
Beispiel c = +1:
0 + 1 = 1
1² + 1 = 2
2² + 1 = 5
5² + 1 = 26 ...
Diese Folge divergiert, die Zahlen sind schnell außerhalb der vorgegebenen Grenze, d.h.
c = +1 gehört nicht zur Mandelbrotmenge.
Beispiel c = -2:
0 + (-2) = -2
(-2)² -2 = 2
2² -2 = 2 usw.
Die Folge ist sofort beim Wert 2, bleibt da, die Werte sind aber nicht kleiner als 2, d.h. c = -2 gehört gerade nicht mehr zur Mandelbrotmenge
Beispiel c = -3:
0 -3 = -3
(-3)² -3 = 6
36 -3 = 33 ...
Die Folge divergiert, ist sofort weiter als 2 vom Urspung weg, c = -3 gehört nicht zur Mandelbrotmenge
Beispiel c = -i:
0 -i = -i.
(-i)² -i = -1-i
(-1-i)² -i = 1 +2i + i² -i = i
i² -i = -1-i, usw...
Es entstehen abwechseln i und -1-i, beide Punkte sind dichter als 2 am Ursprung, c = -i liefert also einen Punkt auf der Mandelbrotmenge. Es ist ebenfalls ein zweier Grenzzyklus.
Beispiel c = i:
0 + i = i
i² + i = -1 + i
(-1+i)² + i = i usw.
Auch hier entsteht ein zweier Grenzzyklus, beide Zahlen sind näher als 2 am Ursprung, c = i gehört auch zur Mandelbrotmenge..
Dann haben wir ja schon ein paar Punkte der Mandelbrotmenge gefunden.
Versucht noch mehr zu finden...
Wie ist es mit c = -0.23 + 0,8*i?
Ich bereite schon mal die Zeichnung vor...
und wenn ihr eure erste Mandelbrotmenge gezeichnet habt, kommt der nächste Post....
Wir beschäftigen uns wieder mit unserer Gleichung z(n+1) = z(n)² + c mit komplexen Zahlen.
Zur Erinnerung: Eine Juliamenge Jc gehört zu einem bestimmten Wert von c und enthält die Startwerte, für die gerade noch eine Konvergenz der Folge von Zahlen z(n) vorliegt.
Jetzt nehmen wir einen festen Startwert, nämlich die reelle Zahl z(0) = 0. Wir arbeiten mit den Konstanten c, für die die Folge der Zahlen z(n) beschränkt bleibt, also z.B. |z(n)| < 2.
Ich hab mir das mal in ein Schema aufgeschrieben:
In einer zu c gehörenden Juliamenge werden also bestimmte Startwerte aufgetragen.
In der Mandelbrotmenge (sie gehört immer zum Startwert 0) werden bestimmte Konstanten der Folgen aufgetragen.
Über meinem Text stehen die Bedingungen zum Auftragen.
In den folgenden Rechnungen schreibe ich die ersten Folgenglieder der Folge z(n) hin:
Beispiel c = 0:
0+0 = 0,
0+0 = 0, usw.
c=0 liefert also eine beschränkte Folge, sie bleibt imemr auf dem Startwert hängen, der auf dem Urspung liegt.. Der Punkt c =0 gehört zur Mandelbrotmenge.
Beispiel c = -1:
0 - 1 = -1,
(-1)² + (-1) = 0
dann: -1, 0, -1, 0...
c= -1 liefert zwei Endwerte, die abwechselnd angenommen werden und die nicht weiter als 2 vom Urspung entfernt liegen. Der Punkt c = -1 gehört zur Mandelbrotmenge. Man sagt, er gehört zu zwei Grenzzyklen.
Hinweis: c = -1 ist eine komplexe Zahl mit dem Realteil -1 und dem Imaginärteil 0.
Beispiel c = +1:
0 + 1 = 1
1² + 1 = 2
2² + 1 = 5
5² + 1 = 26 ...
Diese Folge divergiert, die Zahlen sind schnell außerhalb der vorgegebenen Grenze, d.h.
c = +1 gehört nicht zur Mandelbrotmenge.
Beispiel c = -2:
0 + (-2) = -2
(-2)² -2 = 2
2² -2 = 2 usw.
Die Folge ist sofort beim Wert 2, bleibt da, die Werte sind aber nicht kleiner als 2, d.h. c = -2 gehört gerade nicht mehr zur Mandelbrotmenge
Beispiel c = -3:
0 -3 = -3
(-3)² -3 = 6
36 -3 = 33 ...
Die Folge divergiert, ist sofort weiter als 2 vom Urspung weg, c = -3 gehört nicht zur Mandelbrotmenge
Beispiel c = -i:
0 -i = -i.
(-i)² -i = -1-i
(-1-i)² -i = 1 +2i + i² -i = i
i² -i = -1-i, usw...
Es entstehen abwechseln i und -1-i, beide Punkte sind dichter als 2 am Ursprung, c = -i liefert also einen Punkt auf der Mandelbrotmenge. Es ist ebenfalls ein zweier Grenzzyklus.
Beispiel c = i:
0 + i = i
i² + i = -1 + i
(-1+i)² + i = i usw.
Auch hier entsteht ein zweier Grenzzyklus, beide Zahlen sind näher als 2 am Ursprung, c = i gehört auch zur Mandelbrotmenge..
Dann haben wir ja schon ein paar Punkte der Mandelbrotmenge gefunden.
Versucht noch mehr zu finden...
Wie ist es mit c = -0.23 + 0,8*i?
Ich bereite schon mal die Zeichnung vor...
und wenn ihr eure erste Mandelbrotmenge gezeichnet habt, kommt der nächste Post....
Sonntag, 3. Mai 2020
Teil 7: Julia Mengen II
Wir wollen nun lernen, was die bunten graphischen Darstellungen einer Julia Menge bedeuten.
Fall c=0:
Fangen wir mit dem Fall c = 0 an, wir haben also z(n+1) = z(n)².
Es gibt genau drei Möglichkeiten, wie sich die Folge von Werten verhält:
Entweder alle Werte (bzw. die Beträge der komplexen Zahlen) streben zu 0, ins Unendliche oder der Betrag bleibt |z| =1, d.h. sie bleiben auf dem Einheitskreis.
Streben die Werte gegen 0, sagt man: Die Folge aus Zahlen konvergiert.
Streben die Werte gegen Unendlich, sagt man, dass die Zahlenfolge divergiert.
Liegt eine komplexe Zahl auf dem Einheitskreis, dann ändert sich durch Quadrieren nie ihr Abstand zur 0, lediglich der Winkel wird verdoppelt, d.h. mit jedem Schritt wandert die Zahl auf dem Einheitskreis herum, bleibt aber dort.
Es gibt also zwei Fälle:
Alle Startwerte, die zu einer konvergierenden Zahlenfolge führen, liegen im Einzugsbereich E, alle, die zu einer divergierenden Zahlenfolge führen liegen im Divergenzbereich D.
Die Julia-Menge ist genau die Grenze, sie enthält also alle Startwerte, die gerade noch zu konvergierenden Folgen führen. Sie ist der Rand von der Menge E.
Für unseren Fall ist also klar: Für c = 0 ist die Juliamenge die Kreislinie des Einheitskreises.
Ganz oft gibt es keine mathematischen Gesetzmäßigkeiten, aus denen man das Verhalten der Zahlenfolgen bestimmen kann. Dann legt man eine Grenze fest. Sobald die Zahlenfolge diesen Wert überschreitet, gilt der Startwert als zu D gehörend.
Jetzt kann man noch schauen, wieviele Rechenschritte (Iterationen) man machen musste (wie groß also das n ist, ab der die Grenze überschritten wird) und dann kann man je nach Größe von n dem Startpunkt eine andere Farbe geben.
So entstehen die sich umfassenden farbigen Bereiche...nach Außen überschreitet die Folge immer schneller die vorgegebene Grenze. der innerste dunkle Teil ist dann die Juliamenge.
Die Julia-Menge selbst enthält immer überabzählbar viele Punkte, sie ist also gleichmächtig zur Menge der reellen zahlen. Kann man bei diesem fragilen Gebilde kaum glauben...
Sie sehen fragil aus, sind aber sog. dichte Mengen.
Das erkläre ich am besten an einem einfaschen beispiel: Die Menge der Brüche liegt dicht in der Menge der reellen zahlen. Ihc kann jede irrationale Zahl beliebig genau durch einen Bruch (rationale Zahl) annähern.
Wenn jemand von euch π auf 500 Stellen genau kennt, dann weiß er oder sie wovon ich rede...
π = 3.1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679 8214808651 3282306647 0938446095 5058223172 5359408128 4811174502 8410270193 8521105559 6446229489 5493038196 4428810975 6659334461 2847564823 3786783165 2712019091 4564856692 3460348610 4543266482 1339360726 0249141273 7245870066 0631558817 4881520920 9628292540 9171536436 7892590360 0113305305 4882046652 1384146951 9415116094 3305727036 5759591953 0921861173 8193261179 3105118548 0744623799 6274956735 1885752724 8912279381 8301194912 …
Eine Anmerkung sollte ich machen: Wir arbeiten mit komplexen Zahlen, da haben wir gesehen, dass man keine Anordnung machen kann, also nicht sagen kann, wann eine komplexe Zahl größer als eine andere ist. Hier meint man immer den Betrag, also den Abstand zur 0 oder den Betrag der Differenz zweier komplexer Zahlen.
Fall c= i
Wir betrachten also jetzt die Folge z(n+1) = z(n)² + i und versuchen wieder herauszufinden ab welchem n die Zahlen (bzw. ihr Betrag!) eine gegebene Grenze überschreiten (meistens 2).
Was herauskommt habe ich in einem kleinen Film zusammengefasst, der einzelne Iterationsschritte zeigt und am Ende die Julia-Menge und ihre farbig markierte Umgebung.
Solche Simulationen kann man mit dem Programm fractale Extreme selbst machen, für drei Wochen gibt es eine Testversion, danach muss man etwa 10.-€ zahlen.
(Fall ihr den falschen Film, einen früheren, seht: Browser beenden, bereinigen und neu starten...)
Fall c = -0732 + i*0,241
Das wird wohl kaum jemand per Hand gerechnet haben...
Hier die Juliamenge dazu . Ich bin in Bild 2 bis 4 imemr weiter in das jeweilige Bild hineingezoomt und wir erkennen, was fraktale Struktur bedeutet. Immer wieder taucht das gleiche Motiv auf.
Weitere Beispiele:
oben links: c = i, oben rechts: c = -0,4 + i
unten links: c = -0,7 + 0,3 i, unten rechts: c = -1,77 + 0,01 i
Wer jetzt schon staunt, sollte warten... im nächsten Post machen wir mit der Gleichung f(z) = z² + c noch ganz andere Dinge...
Fall c=0:
Fangen wir mit dem Fall c = 0 an, wir haben also z(n+1) = z(n)².
Es gibt genau drei Möglichkeiten, wie sich die Folge von Werten verhält:
Entweder alle Werte (bzw. die Beträge der komplexen Zahlen) streben zu 0, ins Unendliche oder der Betrag bleibt |z| =1, d.h. sie bleiben auf dem Einheitskreis.
Streben die Werte gegen 0, sagt man: Die Folge aus Zahlen konvergiert.
Streben die Werte gegen Unendlich, sagt man, dass die Zahlenfolge divergiert.
Liegt eine komplexe Zahl auf dem Einheitskreis, dann ändert sich durch Quadrieren nie ihr Abstand zur 0, lediglich der Winkel wird verdoppelt, d.h. mit jedem Schritt wandert die Zahl auf dem Einheitskreis herum, bleibt aber dort.
Es gibt also zwei Fälle:
Alle Startwerte, die zu einer konvergierenden Zahlenfolge führen, liegen im Einzugsbereich E, alle, die zu einer divergierenden Zahlenfolge führen liegen im Divergenzbereich D.
Die Julia-Menge ist genau die Grenze, sie enthält also alle Startwerte, die gerade noch zu konvergierenden Folgen führen. Sie ist der Rand von der Menge E.
 |
| mathe ch |
Für unseren Fall ist also klar: Für c = 0 ist die Juliamenge die Kreislinie des Einheitskreises.
Ganz oft gibt es keine mathematischen Gesetzmäßigkeiten, aus denen man das Verhalten der Zahlenfolgen bestimmen kann. Dann legt man eine Grenze fest. Sobald die Zahlenfolge diesen Wert überschreitet, gilt der Startwert als zu D gehörend.
Jetzt kann man noch schauen, wieviele Rechenschritte (Iterationen) man machen musste (wie groß also das n ist, ab der die Grenze überschritten wird) und dann kann man je nach Größe von n dem Startpunkt eine andere Farbe geben.
So entstehen die sich umfassenden farbigen Bereiche...nach Außen überschreitet die Folge immer schneller die vorgegebene Grenze. der innerste dunkle Teil ist dann die Juliamenge.
Die Julia-Menge selbst enthält immer überabzählbar viele Punkte, sie ist also gleichmächtig zur Menge der reellen zahlen. Kann man bei diesem fragilen Gebilde kaum glauben...
Sie sehen fragil aus, sind aber sog. dichte Mengen.
Das erkläre ich am besten an einem einfaschen beispiel: Die Menge der Brüche liegt dicht in der Menge der reellen zahlen. Ihc kann jede irrationale Zahl beliebig genau durch einen Bruch (rationale Zahl) annähern.
Wenn jemand von euch π auf 500 Stellen genau kennt, dann weiß er oder sie wovon ich rede...
π = 3.1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679 8214808651 3282306647 0938446095 5058223172 5359408128 4811174502 8410270193 8521105559 6446229489 5493038196 4428810975 6659334461 2847564823 3786783165 2712019091 4564856692 3460348610 4543266482 1339360726 0249141273 7245870066 0631558817 4881520920 9628292540 9171536436 7892590360 0113305305 4882046652 1384146951 9415116094 3305727036 5759591953 0921861173 8193261179 3105118548 0744623799 6274956735 1885752724 8912279381 8301194912 …
Eine Anmerkung sollte ich machen: Wir arbeiten mit komplexen Zahlen, da haben wir gesehen, dass man keine Anordnung machen kann, also nicht sagen kann, wann eine komplexe Zahl größer als eine andere ist. Hier meint man immer den Betrag, also den Abstand zur 0 oder den Betrag der Differenz zweier komplexer Zahlen.
Fall c= i
Wir betrachten also jetzt die Folge z(n+1) = z(n)² + i und versuchen wieder herauszufinden ab welchem n die Zahlen (bzw. ihr Betrag!) eine gegebene Grenze überschreiten (meistens 2).
Was herauskommt habe ich in einem kleinen Film zusammengefasst, der einzelne Iterationsschritte zeigt und am Ende die Julia-Menge und ihre farbig markierte Umgebung.
Solche Simulationen kann man mit dem Programm fractale Extreme selbst machen, für drei Wochen gibt es eine Testversion, danach muss man etwa 10.-€ zahlen.
Fall c = -0732 + i*0,241
Das wird wohl kaum jemand per Hand gerechnet haben...
Hier die Juliamenge dazu . Ich bin in Bild 2 bis 4 imemr weiter in das jeweilige Bild hineingezoomt und wir erkennen, was fraktale Struktur bedeutet. Immer wieder taucht das gleiche Motiv auf.
 | |
| c = -0732 + i*0,241 |
Weitere Beispiele:
oben links: c = i, oben rechts: c = -0,4 + i
unten links: c = -0,7 + 0,3 i, unten rechts: c = -1,77 + 0,01 i
Wer jetzt schon staunt, sollte warten... im nächsten Post machen wir mit der Gleichung f(z) = z² + c noch ganz andere Dinge...
Abonnieren
Kommentare (Atom)